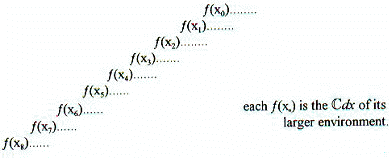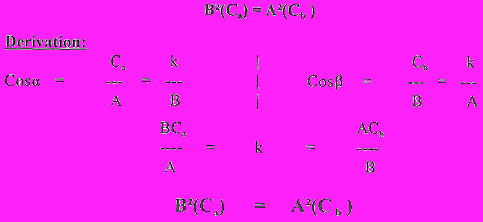Abstract:
Primary versions of complexity to date have been considered relative to fractal models. They have tended to show that complexly ordered patternings arise or emerge after massive iterations of some relatively simple functions which, on their face, do not indicate that important relational and temporal patternings are nascently inherent in them. Corollary work (Prigogine, et al) has shown that in some cases contra-entropy plateaus of stability exist far from initial equilibrium conditions, giving secondary and tertiary conditions on which to build complex systems. These are important and pervasive factors of complexity.Yet, complexity can also be seen in situations which do not involve inordinate membership or interaction samples, and also, in situations that are not easily assessable by equilibrium statistics. It is the author's contention that there also exists a more general and robust form of complexity generating mechanism denotable in simple systems with non-homogeneous construction (that is, in systems which have independent yet interactive sub-components). These sub-components can be evaluated with their own behavior-space, independent from yet interactive with the behavior-space of the system at large.
To accomplish an evaluation of the relationships involved between these diverse behavior-spaces, the original concept of entropy is reconsidered and amended to accommodate multiple simultaneous base-reference frames. Entropy - the dis-ability to do work - is viewed as a measure of spacetime separation among local system membership: the further members are from each other, the less likelihood they will heisenbergly interact ...transfer energy .... "work" on one another.
When mass-momentum energy is spatially confined in smaller regions, the time/space required to get to other energies and to "do work" is reduced. Conversely, when the mass-momentum is allowed to exist in a larger space - by whatever and any means or mechanisms - then the relative local entropy of the mass-momentum has been increased -- relative to its prior conditions/restrictions/states. The time and distance required to get-to-the-next-interaction intersection has been increased. This is a relationship between a membership and its spacetime, defined by variable boundary conditions, even if the membership is "one".
When such energy/information is entropically so-redistributed among two or more agent systems (being themselves factors that enter into defining the behavior space of the sub-energy or information), then the behavior of those agent-systems becomes bound, complex, with their relative entropy decreased. This presentation explores the inverse entropy relationship between nested adjacent reference frames, denoting this interaction as the more robust and pervasive mechanism of complexity.
Complexity: Orchestration of Multiple Stochastic Systems
Complexity is how the universe builds organizations of wondrous intricacy. We recognize it when we see it. We even have mathematics that can model some of it. Yet something is missing. There must be another dynamic at work, one not so subtle or fragile as fractal emergence, to account for Complexity's extraordinary pervasiveness. Something robust. A non-fractal mechanism that is companion to the fractal one.
Formal work on the Integrity Paradigm began circa 1965, prior to fractal math, chaos & Complexity. Its ambitious goal was the formulation of an umbrella theory that would account for the rising of neg-entropic systems, at a time when modern physics firmly pointed to an energy dissipating Carnot universe. In today's terminology -- why order emerges from chaos.
Insulated from the mathematical discoveries of the 1970's and 80's, work focussed on comparing various systems and evaluating how they process energy and utilize information. A pattern began to display itself in every system evaluated. When modeled in a hierarchy which distinguished layers of organization, one in relation to others, it became apparent that behaviors in adjacent layers alternated in their directions of entropy flow. That is, if any membership of a given level dissipated entropically, the typical result would be an induction of anti-entropy order-consolidation on the next larger scale of organization. Conversely, negentropic activity in one, corresponded with entropy in the next. Specific mechanisms were of no consequence, only the resulting relationships, which shone through with extraordinary regularity.
| return to top |
Redefining the general structure of Mathematics
This is the premiere observation of Integrity Dynamics, the notion signaling a shift away from Fractal seniority, paralleling the shift from a Ptolemeic to Copernican solar system. All the remaining work which details the architecture of Integrity Dynamics -- both mathematically geometric and behaviorally expressive -- stems from that fundamental observation. The subsequent work is philosophically in-depth and formidable, potently challenging neo-Platonism, Gödel's Incompleteness theorems, and even the supremacy of Fractal Emergence. It demands that mathematics be reconstructed as an architecture of exponentially nested infinities -- Cantorian infinities -- where the entire structure is informationally accessible throughout. Not just a structure of exponential superpowers, but a relationship of information filled domains, dynamically interactive, topologically connected. This means that there are no closed formal boundaries anywhere in mathematics -- only conditional ones, limited by immediate utility and choice. The mathematical universe of nested and coded dimensions is as much an architecture of many-environments as is the physical universe. There are domains in which information bit-sizes vary, differing from bit-sizes in other levels of organization. Yet they are related, and the activities, the behaviors, of that information integrates with and affects information on those other levels. Fractal Complexity is still involved, but is now a sub-dynamic within this new broader organization.
In an era of Relativity, Quantum Mechanics, Cantor's infinities, holography, Zadeh Logic, quark architecture, spread spectrum transmission, Complexity, and the like, we are living in a changing universe. Actually, it isn't changing, we are expanding into it. To go forward with any sense of order we need a correspondingly new philosophy to carry, blend, and embrace the diversity.
| return to top |
The Integrity Paradigm is a philosophy, a weltanschauung, that can satisfy this need. It steps beyond 10,000 years of founding concepts and presents an alternative ... building on foothold ideas of "information", "concept space", "dimensional analysis", "adaptive evolution", and "emergence" ... embracing them under a single compatible vision. The Integrity Paradigm advances the claim that the principle activity of Complexity architecture rests in that singular yet pervasive relationship which exists between "local entropies", interlaced levels of exponentially nested organization, connecting the universe's assemblies of assemblies. They formed in the cooling wake of Symmetry Breaking, and perpetually evolved in the transformations and transactions of information in various co-present bit-sizes.
The Integrity Paradigm requires significant refinements and extensions of a few of our basic math concepts. One broadens the notion of "equals sign", allowing it to mean that the "information content" on either side remains homeomorphicly "identical", even if forms or expressions are isomorphically different. That is, an intrinsic "content potential" is always retained even if expressed differently. Adjustive coding doesn't automatically erase information. Functional-information is contingent upon what option spaces are present, or potentially available or subsequently generated. Revising an option space - such as by alteration of how the information is expressed - can reconstitute specific information and relevance, even from a topologically coded infinitesimally small "point". "Points" are no longer devoid of "content". Such a notion is compatible with superstring topology, going even further, since it infers that Complexity as a dynamic is generated wholly within the metric of natural topological geometry.
| return to top |
Cantorian Infinities: The new topological matrix
The math relationship "exponent" is now defined to represent autonomous yet interrelated infinite domains, where the question then becomes one of determining what information relationships exist between successive exponential domains. There is more involved than just mapping f onto f', one n-dimensional phase space onto another. Each can have an independent entropy. Each can retain "information content" or content potential, even when coded to zero. Holography and sonoluminescence exemplify this relationship. These nested assemblies of phasespace are therefore fully environmental to one another, each exponential level being its own continuum, a functional Cantorian Infinity, with the potential of being utilized as an independent frame-of-reference, or even a correspondent one.
| return to top |
Thematically then, there are two kinds of emergence, not just "fractal". The other is environmental or dimensional emergence. Their differences are obvious. Fractal emergence functions in isolation. Nascent unknown patterns show up regardless of context. Environmental emergence on the other hand, is completely "relational". It is context and interaction driven, as it produces new information and energy organizations. Interactional changes in a given "content" or its relative "option space" will produce new patterns, new assemblies of organization.

| return to top |
Complexity Requirements: 2 communications are enough!
Both are mechanisms of Complexity. But Environmental Emergence is far and away its more pervasive and robust form. In the simplest case, two non-zero probabilities of communication present between two members of a given assembly level are sufficient to enact Complexity. It is the enactment of communication potentials. The communication probabilities corresponding with entropy changes of the data sub-assembly. They directly affect and narrow the information exchanges possible among sources and receptors in the nested assembly. That limits the freedom of interaction of that next larger order of assembly. Communication and interaction is tantamount to an increase of entropy of what is being transferred, and this imposes a reduction in the entropy of the next larger level. It forces neg-entropy there. It forces Complexity. Quite non-fractally.
| return to top |
We can now surpass Gödel's Incompleteness Theorem. There will always be Gödel Limits - content less-than all - but the characteristics superior to quantification are "coherence" and "compatibility"... any information or energy on the far-side of a local Gödel Limit has the potential to be included "inside". What is external is compatible with what is internal. So, we "know something" very specific about parts of the universe and of mathematical space which Gödel says we should have no knowledge. Thus, a Gödel Limit is not so much exclusionary-boundary as it is accessible interface. The event-horizon of a Black Hole is a prime example. Obviously it exists as a transition state separating regions of supposedly incompatible information. But, it's truer importance is as a channel which information and energy can be transduced through. Gödel is not the final word.
Environmental set concepts call into question Plato & Gödel. For Gödel to be 100% accurate there can be no Platonic "ideals". The ideal or set "apple" and the set "colors" are mutually exclusive if we are to be faithful to Gödel. An apple's "color" can only be known by an interaction relationship the set boundary -- its skin -- has with the external environment, and since the skin is a Gödel Limit, those sets are conceptually and existentially isolated.

"Ideal Apple" with environment "Ideal Apple" without environment
(including trans Gödel-limit information) (excluding trans Gödel-limit information)
For a platonic apple to have color, existence must be Martin Buber's dynamic, I-Thou. When environments exist, sets are completable. This holds true even for mathematical systems. As long as they exist in potential context with other possible mathematics, they can be complete. Validation within a closed system is also available. Systemic verification and consistency can be attained by evaluating any and all possible sub-partitions - transitory internal gödel-limits. There is strength in having an infinite number of option sets which are open to review and testing. Any anomalies will always be natural and native, with the distinction of merely being "local" and "conditional".That is, it is valid to reinterpret Gödel's Incompleteness Theorems by saying that as long as there is consistency -- which is one of his criteria in fact -- then local functional validity can indeed exist inside a system with well defined axioms simply because "consistency" is not violated. A system can validate truth or falseness statements, at least locally.
| return to top |
Eigenspace Options: Surviving in real environments
This shift in thought gives us entre' to exploring information relationships between variable sets and their environments. Sustained behaviors require the ability to deal with both the known and the unknown. Action in relation to potential. First off, the initial "memory" of any system is not carried data, but the rules of construction... the fundamental forces, relativity, entropy. They determine activity and action space. Even in the ultra-heat of initial creation, information was already present to enact the products of symmetry breaking and cooling.
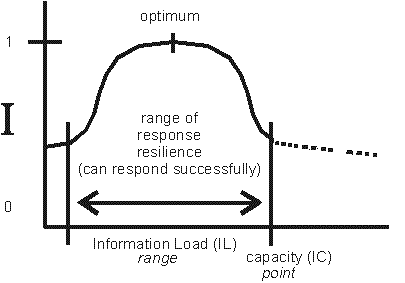
When that cooling occurred, enduring in extended environments required "compatibility" ... the ability to cope with encounters by avoidance or interaction. Self-organized systems therefore need empty eigenstates ... states of "ignorance" if you will ... with the available capacities to encounter new information or energy. Maximum information or energy content therefore is totally antithetical to the health, the integrity, of any dynamic system. It cannot be its "goal". Neither is attainment of ground-states. Isolated ground states isolate a system from behavior potentials. Likewise, rigid determinism over-formalizes systems, lessens survivability because behavioral options are removed. There is nothing efficient or functional about a computer which data storage and operating spaces are saturated. Atoms "survive" not because they settle into unchanging persistent energy configurations (except for quantum variability), but because quantum electron shells are available and are adaptive to changes in energy content. It is an error - though an understandable one - to think that Complexity rides at stability nodes poised between chaos and order. The truth is that Sustained Organization persists posed between too much energy or information, and too little -- with priority placed on the constructive capacity to handle energy and information possibilities. More than sufficient, less than saturation.
INTEGRITY | return to top |
Change in Eigenspace, Change in Entropy
In every complex system imaginable such room-for-change is identifiable as variability-of-entropy, plus or minus. This is crucial. For now we can perceive and evaluate the impact such local entropy changes have in relationship with their surroundings. We discover that the behavior-space of a subset domain of a system alters inversely the behavior-space of its members. The entropies are inversely dynamic and interdependent. And it doesn't matter if the motivating energy or inductive change of phasestate comes from the sub-system or the external environment (that is, quantum mechanical or thermodynamic sources). The relational dynamic holds regardless. This is the crucial concept. Integrity vs Complexity.
A system's Integrity -- its sustained dynamic self organization in extended environments -- is not a state poised between order and chaos, but a functioning option-space poised between determinism and the full statistical potential of much greater self-with-environment behavior space. Even adaptive evolution uses extant mechanisms to find new integrity options -- surviving by changing.
| return to top |
Geometry and activity of Information Topology
The Integrity Paradigm yields some specific, unusual, and very improved intuitions covering a wide range of related topics. I mention them briefly, not in any particular order of seniority.
Statistics and Fields. Ever since the development of quantum mechanics the consensus has been that QM precedes thermodynamics. Integrity strongly asserts the opposite position. Firstly, statistical distribution are behavior sets with the time dimension removed. Temporal events in n-dimensions are reduced to n-1 dimensions - orthogonally mapped, if you will. The action gradient is removed, not absent by default, or normalizable to "one". If no gradient is present enabling behaviors, no statistics get generated. Period. Take a ball bearing peg-board that generates a bell-curve. Remove it from a gravity well. Nothing happens. Some prerequisite action potential must be present in any and all cases where statistical accumulations occur.
G not just Sigma~function, but Gradient(Sigma~function)
Also, the energy and information throughputs must be process-compatible with the structure and energy/information handling capacities of the system it transits. Changes in internal structure, or changes in throughputs, can generate significantly different distribution "curves". For example, instead of dropping ball bearings or marbles through a peg-board matrix, to generate a gaussian curve, drop a bowling ball. The 'curve' is a vertical line. I.e., under 'ideal' and contrived circumstances we can generate utilitarian fundamental 'rules'. But, we must expand any mathematical formulations to allow for other 'internal' variations of construction. We become aware and sensitive to the fact that there may be families of rules and responses when we adjust the energy and information units which any given system processes. Given a single peg (again, in a reference gravity field), with minor lateral variability of small ball bearings bouncing down on it, the resulting 'curve' will be two separate piles, skewed out on either side. Reminiscent of fractal attractor-basins; and otherwise, of binarily symmetric Hamiltonian distributions.
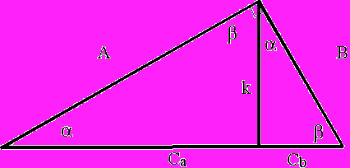
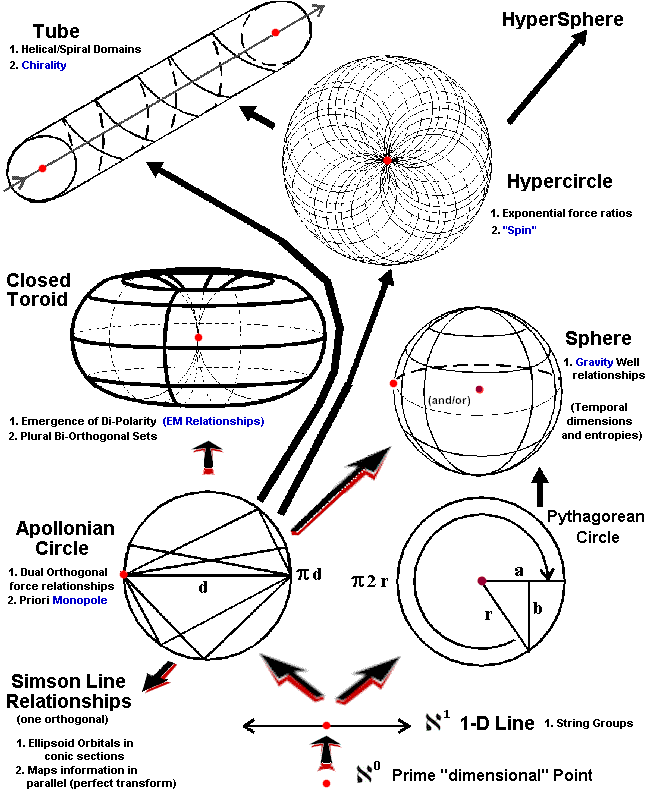
Topology of an Information Universe. There is a companion system to Pythagorean trigonometry which was first noted by one of his contemporaries, Apollonius. The reference base of a circle (and thus all wave functions) is no longer some central focal point. A circle or wave function is also generated by twin orthogonal conditions stemming from an originating "point" (of dimension zero), out along any linear extension of dimension-one. The point persists as "endpoint", not midpoint, of the one dimensional object.
Several interesting things arise from this. First, the relationship A2Cb = B2Ca occurs, derived from the Law of the Excluded Middle and Law of Cosines. When changed to [DeltaA2/DeltaCa = B2/Cb] and the "A" side is taken towards zero, the ratio tends toward "one", generating the Cantorian equality, where the Aleph infinity of a line is equal with the Aleph infinity of a plane.
Also, progressive derivatives or integrations of the basic sine function merely reproduce the same wave-curve, simply shifted 90 degrees. That is, the "information" is retained, complete and intact. The unavoidable conclusion is that all calculus functions accomplish the same thing ... information is constant even though its form is mutable and codifiable in many different ways.
Many interesting things happen under this new view of information.
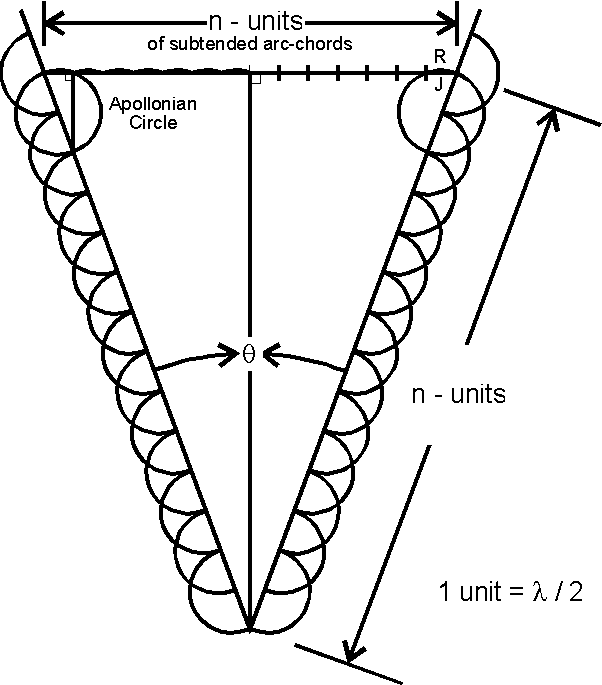
If we take this relationship and map it as wave functions out from the vertex of an acute angle, we find two things. First, that the number of one-half wave units along each side generates the same partitioning along an orthogonal line perpendicular to the mid-line of the angle ... regardless of the size of the angle! This means that the "information content" of the orthogonal domain is consistently identical with the information "n" of "n(lambda/2)" , no matter how small the angle gets ... even reduced to zero. Perfect orthogonal transference of information This is dimensional coding/compression. This is the foundation of holography and sonoluminescence.
Perfect orthogonal mapping of information "n" regardless of angle theta. Even if the angle Theta equals zero . . . that is, even if the wave-function collapses to a "point".
The second result comes when we evaluate the smallest state of orthogonal information-bit transcription ..."one" generating an orthogonal "one". The base state is lambda/2 , and is represented by an equilateral triangle inside a circle. Keeping in mind that this geometry represents several co-present states of symmetry, we note that if we rotate the wave function around its internal axis of symmetry until it maps-itself, so to speak, these mappings come in units of +/- 1/3 and 2/3. We now have a situation which conjoins "halves" and "thirds" ... the underlying symmetry of quark architecture, where the "thirds" are present and real, but are transcendently "relational". That is, they are functionally intrinsic factors, but have no "independent identity" or "physical reality" outside the enactment of the architectured process.
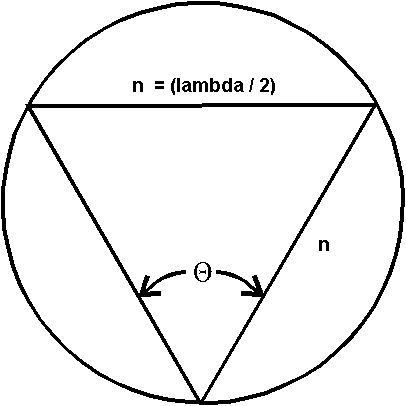
Spatial (rotational) symmetry of thirds.
Wave (8/2) symmetry
of halves.
Information symmetry of units.
The arc segments scribed out along the vertex angle (from the initializing "point" at the bottom of the figure) correspond with wavelengths (8 / 2), which work as the units-of-information in this brace of relationships. Coupled with the rotational symmetry of thirds (in this planar scenario), there exists an embedding of symmetries in the basic geometric topology of the universe. The resonances which can be constructed from this correspond with quantum renderings of particles and atoms, as well as the orthogonal relationships of electro-magnetism.