
To Mathematics and Beyond
I started examining how fluencial (dimensional) relationships are approached in current mathematics, and because I tend to rely upon geometric imagery so much, I looked at how a Cartesian straight line relates to the next higher fluencial form - the circle.
The classic relationship is "squaring a circle" and vice versa. In modern context, this leads to trigonometry and so forth. But, instead of concentrating on letting line segments float around a 0,0 focus - because this would be letting the radius-segment "be" one-fluencial in a two-fluencial continuum, I assumed a subtle restriction....to let the curve called "circle" be the representative of an information quantity in 2-fluence, and see how it compared to the line-segment, which is an information quantity in 1-fluence. Comparative topological mapping. It turns out to be no trivial way of examining them.
A line segment "compares (maps) into" 2-fluence in an orthogonal direction. In this simplistic form of example, the "information quantity" of a quarter-circle arc, would compress, or translate into, a 1-fluensial line segment having a value quantity which is the radius of the circle. It is apparent that the tangent differentials go from 0 to infinity, around the curve, but I want to focus on specific value translations for the forms themselves. From the perspective of an x-axis, seen at (0,0), at x=0 y=r, the curve obviously has an information content (length) of zero. Likewise, at y=0 x=r, the curve has an information content of p/2 (since, relative to r, the measure of the full circle is 2p, and 1/4 that gives p/2). The midpoint of the quarter-arc, p/4, has a wonderful simultaneous translation into both/either the x and y axes: one over the square root of 2; (1/Ö2)!
Assuming there to be a valid Operator-function, Ä , that multiplies the two 1-fluence (Cartesian) values to equate (translate) to a single 2-fluence (radial/circular) value, the formula would look like this:
1/Ö2 Ä 1/Ö2 = p/4 (eq.1)
Vectorally, the multiplication of two 1-fluencial continuums gives one 2-fluencial continuum. In this comparative translation, one over the square root of two <1/Ö2>, squared, "equals" (transcribes to) p/4. If we assign the appropriate orthogonal fluence to each root-form on the one side on the equation (X,Y) , and correspondingly, assign a similar kind of singular 2-fluencial labeling to the p/4 side....say "h"...just to pull a random symbol out of the air, then, what we have is......Heisenberg's Uncertainty Principle! (utilizing Plancke's constant).
If we replace (x,y) by (p,q)<momentum,location>, lets examine Heisenberg's formula:
Dp · Dq ³ h/4p (eq.2)
Now, in Heisenberg's 1927 letter to Wolfgang Pauli where he derived the uncertainty relations for p and q, he defines
p1=Ö2Dp and q1=Ö2Dq.
thus: p/Ö2 · q/Ö2 ³ h/4p (eq.3)
Which is an expression of :
(1p1/Ö2) · (1q1/Ö2) ³ (p /p) (h /4p) = (p/4) (h /p2) . (eq.4)
| Equation 1 and Equation 4
are linguistic equalities of each other. (!) where (h /p2) is the more accurate topological rendition of the Planck limit. This value is a prominent constant in Z.P.E. equations. |

Theorem |
Heisenberg Uncertainty Principle |
|
1y/Ö2 Ä 1x/Ö2 = p/4 (of unwritten parameter) bi-Cartesian function = Radial function Note: In the normative case r=1. However, evaluating the equation as an expression of a Euler formula "r" could be set equal to p. (see reference below) Note: If scalarity of the Cartesian components are allowed to float, the limit translations become "relativistic". Note: Conformal topological "mapping" is a related topic to understanding the dynamics of information translation between "dimensions" (aka: fluences) |
Dp · Dq ³ h /4p (where:
Dp = p1/Ö2, Dq = q1/Ö2)
replacing p1=y
q1=x y/Ö2 · x/Ö2 ³ p/4 · h/p2 1/Ö2 · 1/Ö2 ³ p/4 · (h/p2) INTERPRETATION of the U.P. Note: The "statistical" domain becomes a smooth unbroken fluencial continuum. That is, quantization exists in a differentiable but non-quantized "environment". |
Parenthetically, hopefully not muddling the waters too much, the final term above (Plancke's Constant divided by p2) is a clue whose meaning can be coordinated with the phenomena of the ratio of the mass of a proton to the mass of an electron, 6p5. They both refer to fluencial information comparations. They indicate that fluencial domains are factors of pn. I will discuss this aspect later. Suffice it to say that Pi can be correlated to all fluencial geometric forms. If we allow Pi to become our base "unit" of reference, rather than "one", then beginning with "kp0" as a fully dimensional "point" we can generate geometric representations of all 4 "fundamental" forces. By fluencial (dimensional) integration we can generate (in 6-fluence) the proton/electron mass ratio, and key into the degrees of electron spin, 720o. The indication is that Pi <p> in this sense is actually part of the operator <Ä> ffunction rather than a transcendental ratio-relevant "number".
So. Heisenberg's Uncertainty Principle is in actuality a statement about information translation between different forms of fluencial expression. Co-assignment of a label, in this case Planck's constant, merely fixes the relationship to the empirically measured fluences of atomic structure. It needs to be remembered though, that at this point in our understanding, there is nothing that restrict's that constant from being any variable value. Mathematically, not measurably. At some point in our search, years into the future, we will discover that the various special Constants of universal structure have a causal source. And the values that we painstakingly measured to determine, are actually prescribed from other more primal relationships in the fabric of space/time/energy (nee "information").
Besides separating out determinability of the components of momentum and location, the Uncertainty Principle also specifies the explicit region of function for these factors and thus creates the statistical domain of extancy for each and both. Relational values for tangents to the curve, establish relativity-pertinent values. All are Information relationships.
This, at the core, is what our mathematics, is all about. The "equality" ffunction is an information link/transfer mechanism, joining and evaluatively comparing, transcribing, information quantae between fluencial values that are just expressed in different ways.
"So what?" you ask. We all knew that. There is nothing special or important about stating the obvious! I beg to differ. There is great importance. Go to any dictionary you can find. It will not have the correct definition for the word "flying"! Surprised?! Don't be. You'll find a list of examples but you will not find a "definition" ...the encompassing thema we think of when we say/think "flying". You will not find the overriding mental image that allowed humanity to strive to "conquer the skies". And this is absurd in an age when we are scooting through the atmosphere, and "winging" it through the solar system ... and beyond! What should be there is : "controlled motion through a gaseous medium"! THAT, is the definition of flying that encompasses all life forms and all mechanical apparatuses that accomplish the act. THAT is what humanity (not just 'man' <sic>) had striven for, for centuries, and finally achieved. The point that I am urgently making is that we should not take accepted concepts for granted. In this case, a mathematical relationship may have been functionally satisfactory but not exactly perfectly correct.
What we say, and how we say it, has incredible importance for us. We must be more clearly explicit when we notice important qualitative distinctions. Such is the case with the current language of mathematics. It requires some fine tuning at the most fundamental levels.
That is why it is crucial for us to make adjustments in the linguistic structure of Mathematics. To make sure that it conveys (transcribes) exactly what we understand and mean. To make improvements that don't leave the message an "implied" one....as in the case of the old and weak "definition" of flying. What we say....how we say it... is important!!!
We return again to discussion of the line segment/circle arc relationships. Since we restricted ourselves from allowing the radius line segment to "sweep out" a circle, how then can we expect to get from 1-fluenciality to 2-fluenciality? We could continue to do it with Pythagoras. But, it is better for us to use his contemporary, Apollonius!
Consider a Euclidean-Cartesian straight line segment. Instead of holding an endpoint fixed as a "focus" and finding a 2-"dimensional" circle (being the set of all loci possible for the other endpoint), rather, we specify that the segment remains at-all-times "fixed" as a hypotenuse of a triangle whose remaining two sides meet always and only at a right angle. The resulting grouping of "points" in this case will be ..... a circle. Exactly as in the Pythagorean technique. Without the necessity of actually moving a "1-fluence" through a 2-fluencial continuum, we can get the same result by determining a set of loci in 2-fluence, linked by other 1-fluencials that severally translate the "information" of a line-segment "into" (1+1)-fluences.
Imagine that you are looking at a sheet of paper cut into a perfect circle. Slowly turn the paper until you can only see it edge on. You have effective "compressed" a two-fluencial into one!!! In fact, the only time you view a "perfect" circle when looking at that paper is when the 2-fluencial surface is absolutely perpendicular to your line of sight... orthogonal. Via Apollonius, the situation occurs whereby a 1-fluencial line segment "arises" the next highest 2-fluencial form...a circle. All, based upon a specific continually connected group of lines which coordinate to generate the next-fluencial form.
Recalling that the Pythagoras Theorem places all component linear
measures into relationships referential to only 2-dimensionality, I started to examine
Apollonius to see if it would be possible to separate and differentiate the
fluencial-hierarchies. It is.
We can accomplish it by using what I have jumped to claim for my own as "'s Theorem". (Of course, when someone shows me that a Greek geometrist already stated it 3,000 years ago, I'll gladly hand back the crown. Until then, I'll just have fun with it for a while! ... If all this can't be fun too, then the Universe isn't the joyful fantastic Creative Essence I believe it to be!)
's Theorem: For any right triangle with sides A,B and
hypotenuse C,
a+b= 90o,
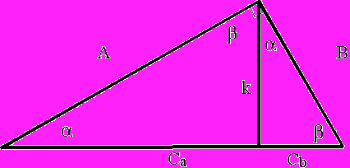
An altitude from the intersection AB connected orthogonally with
C, produces this net relationship:
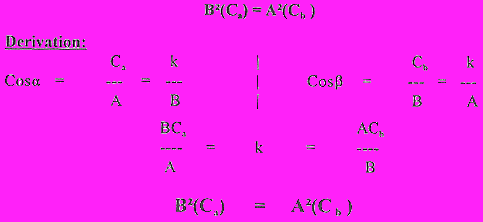
The reason this relationship is so important is because it is desirable
to keep at least one line segment in its original 1-fluencial form,
and this expression does just that. C, as hypotenuse, stays "one-fluencial".
And its second-fluencial comparators (A,B) are expressed strictly in that way: 2-fluencially.
This in fact, is the relationship that specifies and reinforces "orthogonality".
The relational formula is highly dependent on two co-extant orthogonalities:
the right angle where A meets B ; the right angle where k meets C. The domain which
connects the separate values and acts as a translating "lens" is the mutual
value "k", which corresponds in general to "wave amplitude"
(which remains "equal" when referenced from any location around the
ffunctions ... almost on a par with the relativistic velocity "c" of
the speed of light). In a tensor-metric sense, values are fixed throughout the remaining ffunctional
domains regardless of how near or far from any specific locus under consideration.
A crucial adaptation of seminal relationships opens itself up for us at the rewritten Limit-form of the equation, when either A or B approaches ("becomes") zero, in the sense of the Calculus De. Instead of the whole equation being reduced to "0 = 0", we treat the values as differential integrals "Delta A, Delta Ca, B, Cb ". We bring both deltas to the same side of the equation, and instead of (DA)2 and DCa becoming "zero", they are allowed to vanish infinitesimally ... approaching a 1:1 correspondence.
B2
DA2
--- = -----
C b D(C a)
As both Delta's approach zero, the ratio approaches unity.
Result: an apparently fallacious anomaly. C b = B2 ?!?!?!?!
Before you disregard this as absurd, wait!! Consider what I am discussing here. I am not speaking about equating "values" in a single continuum or fluence (where 5 can never equal 25, obviously!). I am speaking about comparative information content in distinctively written fluencial forms! More in the sense of topological homology...where a domain can be "distorted" yet remain unaltered as a self-consistent region. A qualitative equality-translation is in force here. As already shown by Cantor, the two seeminging different infinities (C; B2) are really identical.
The above equation, anomalous per "one-fluencial" domains, exhibits reasonable and consistent meaning in comparisons of "poly-fluencial" domains (an environment of fluencial Continuums).
{Information Content} of a One-fluence
"equals" (Translates to - via ffunctions of compression or expansion)
{Information Content} of a Two-fluence
This is the same basic distinction we found in the new interpretation of Heisenberg's Uncertainly Principle. What this "equality" indicates is that there is an interfluencial operator present which has not
been explicitly expressed before.
Let's recall Whorf's conceptions concerning perception and language ... experience translated and recodified...and look at "equations" in that way. A mathematical equation is a mechanism, the foundation of which is a relationship. The mechanism has its own connected relevance to each statement on either side of the equality (sameness) sign, before and after the mechanism (operation) is applied. But, it is not the relationship of, or between the (at least two) statements (conditional self-relationships).
This is an odd distinction to make, but it is an important one. For it allows the existence of a "relationship" whether or not it can be stated mathematically. Mathematics and mathematical equations can be thought of as ffunctions of information. An equation is an information "translator" in that it changes specific information from one form to another.
Secondly, it stops us from saying that the mathematics is the relationship. It is not. It is the description of a relationship. No matter how rigorous and exact a mathematical statement or equation is, it is still only a mechanism, an operator, a translator, which expresses the different forms that relationship of events can take.
This is an important turn for mathematics. The Calculus developed by Leibnitz and Newton devised the use of differentials strictly within single-dimensional-continuums (one-fluences). The apparatus has been intensely used to refer to multiple fluences, but only in singular step-wise fashion. Tensor, metric, and higher "dimensional" manipulations have merely been compressions and expansions of single-continuum forms. At this juncture, we can link Calculus with Topology in more complete ways. Use of D,d,d are correct and meaningful when applied to separate (but intersecting; ie,'connected') continuums at the same time. In other words, where homologous mapping is possible, but where perfectly equal scalarity (strict one to one correspondence) is not necessary. We can phase-shift the operations in order to see what happens simultaneously in nested adjacent (and distant) domains. It is a short-cut validly applicable to Lorentzian transformations, and gets the net-important information across several continuums without requiring a Turing-sequence, or rather, requiring detailed exposition of such sequences. The physicist/sci-fi author James Feigenbaum has suggested I refer to this by the obvious name: Exponential Calculus. The tacit unspoken constraint (Whorf masking) which we are breaking free from the confining chains of is that D rates of change need not be identical for a ratio or differential to approach a real and valid limit.
Priority of the above Theorem is based on the relational ratio of the two values equaling "one", and the inherent meaning that Information content of a "one-fluencially" based function statement is exactly the same as that expressed as a "two-fluencially" based function statement. This is a subtle but important variation on the way we have traditionally treated "information". It differentiates between extant and heterotelic information. We can separate out the information which is extantly "specific" and therefore "variable", compared to the information which - because of the relationship "between" extant-values - remains "constant" even when values vary. There are certain forms of value quantae within given ffunctions which remain constant and, for the most part, get transcribed ahead of a propagating wave-amplitude (like the -Bridge discussed at the beginning ... potential "information" on the "far-side" of a boundary condition ; in this case the potential information is highly deterministic and pre-fixed by the incipient wave {subject of course to future interactions at any next "Heisenberg Intersection"}). The next diagram will illuminate this idea.
The next step which shows how we can be confident about not needing a Turing-sequence, and can freely use poly-fluencial differentials and integrals, is through a fascinating re-interpretation of a "fundamental geometric relationship", made obvious by doing a geometric construction that incorporates the /Apollonian Triangle:
Theorem A2Cb = B2Ca |
 |
Apollonian Circle Radial: Set of all values r , where r = gCosq, |
The Apollonian relationship establishes a very special ability: the immediate and simultaneous translation of information into orthogonal/ perpendicular domains. Regardless of the central angle, theta, the "information" - fixed by the wave length - will always be corres- pondingly transcribed and translated orthogonally. Even as f is brought to (and through) zero, the "information" remains. If we correlate r with temporal fluences then it becomes obvious that the r = zero state is the "particle" form of the wave-ffunction. |
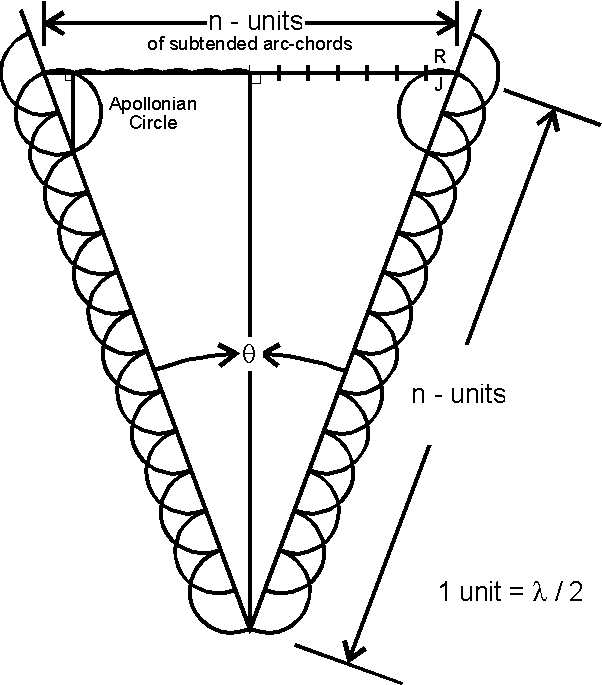 |
1 unit = l/2
We start with a method for dividing the primary vertex angle of an isosceles triangle in such a way as to divide a line perpendicular to the angle's divisor into n-equal parts:
1. Using only a straight edge, draw two lines crossing at any angle. (for ease of example 30
E or less is useful).2. Taking up a compass and starting with the vertex as focus point, mark off along both lines extending out to infinity, "n" number of unit distances of equal measure. Considering practical limitations of a sheet of paper, it's convenient to use 1/2 the diameter of the scribed random-unit circle, with a "n" up to about 25 or so (again, less is easier).
3. Returning to the straight edge, at the points along both lines where the "nth" measure is indicated, draw a line connecting those points. This completes an orthogonal base-line of an isosceles triangle.
Now, let's clearly evaluate the linear transcription of non-linear information forms we just accomplished. The net dynamic result of this construction is that the base line crosses the "nth" circle in a cord "J" under an arc "R" of the circle. The length of the baseline is (nj)!! And more importantly, there are "n" arcs "R"! Pi (as an inter-/luencial ratio) translates quantums into corresponding net-orthogonal /luences without loss of information.
Envisioning the arcs as wave forms, the wave frequency in one net-direction can be, and is, directly transferred into any orthogonal fluence on a one-to-one basis regardless of proportional size differences in the comparative domains. Applying again the differential/integral process of The Calculus, we choose smaller and smaller angles q, until it "vanishes" (according to the methodology). The net result is that the "information" that existed along a continuum having a measurable "extent", is now, in affect, "coded" and "compressed" into a point singularity! With the information content intact. "Torque", "angular momentum" and all similar relationships, are orthogonal transfers.
Wave functions that exist along a specific fluencial path, have a homogeneous corresponding existence in any and all orthogonal fluences. And the information content is retained. This is the foundational principle of Holography. The orthogonal "wave front", at any and all points in the perpendicular plane, holds, carries and maintains, the "information" present in and of the waves along their original paths.
The radial trigonometric expressions of the Theorem of Apollonius are the cosine wave form /unction in 'x' and the sine function in 'y' in all the formulations of orbital mechanics! Apollonius...not Pythagoras ... drives the planets! (There is something historically and mythologically pleasing to describe it this way...a fun musing, if you will...Apollo being the driver of the Solar Chariot (!) in ancient Greece). Parametrically speaking, that is!
Transcription of Cartesian formulae into parametric equations can be understood as an extraordinarily important "translation
A circle "equals" =====> rCosq (rho cosine theta) or rSinq.
Additionally, the 1st derivative of Sinq is Cosq and, the derivative of Cosq is -Sinq !!!!!! The derivatives translate Orthogonally, as well as produce the Negative Right-hand Rule!!! Otherwise known as "spin"!! And, also infers why Gravity is a "negative" aka "attractive" ffunction! It is the negative form of the Left Hand Rule of Energy Transfer! Thus indicating how a force can be a "negatively constructed field" in comparison to matter/energy dynamics which operate "positively" by transfer interactions. More importantly, it is an already known and accepted form-function-relation of the /Apollonian premise : Information content transcribes exactly in orthogonal domains. Here, wave forms phased by 90 degrees.
When using the evaluation approach developed based on a Cartesian co-ordinate system, and applying that reasoning to radial-wave functions, the truth of it becomes obvious: A derivative...in "mathematical" space will translate any and all data and information into any orthogonal "mathematical" fluence (nee: dimension) without any loss of information. The only relational information that needs specification are "Constants". It is obvious that there is a "direction" to the flow of information in all mathematical and existential ffunctions...whereas the derivative of a Constant is "zero", the anti-derivative of "zero" will not specify a particular Constant.
Spin, is a resulting constructive component having its origin in the orthogonal relationships of the derivatives of the wave, as expressed in the construction of a circle - in the /Apollonian method - originating in a point that will end up being ON the circumference of the generated circle, and surfaces of the spheres and toroids, as designated by r=sinq. And thereby, at any point along the sine wave functions. The orthogonal derivatives generate:
 |
Sinq --> Cosq --> -Sinq --> -Cosq --> Sinq -->.....
In a sense, this is a variant restatement of Lorenztian transformations because the information "content" remains constant even though taken through dimensional translations and rotations. The frames of reference are "substituted" but the inherent information remains constant. (!)
This brings us full circle in the methodology discussed at the very beginning of this treatise. To examine and understand what we previously knew, but to appreciate in a new and more complete way. To wit, the derivative of a wave function along one fluencial axis is the wave function along a perpendicular orthogonal axis in a specific direction. Crucially, the "information" is retained intact and is correspondingly translated "into" the orthogonal fluence. And. It can display itself in the form of either another wave or a point. Translation? But of course!
ENERGY INFORMATION QUANTA EXISTS SIMULTANEOUSLY AS BOTH WAVE AND PARTICLE.
The operative word here of course is "simultaneously". When the vertex angle is treated as the descriptor of temporal vectors, then it is obvious that when the Dq is greater than 0 (zero), there is a temporal extent duration, and the information finds expression as a wave. When Dq = 0, then the net temporal vectors balance and compress to an "instant", the information finds expression as a particle.
Ad reductio, when all temporal vectors in the universe reduce to a Singularity, then all information, all energy, does too.
Cept: In this Universe there is no such thing as a "straight line"; it is an artifact of experience and convenience more like an asymptote compares to a variable function. It represents ... and stands as ... a "limit value" or "boundary" between Nested Cantorian Infinities.
Cept No information or energy is translocated in this universe except in "wave" form.
Waves translocate information along a non-point cross section, in a net-direction, but not centered perfectly "point" to "point" locationwise (source to receptor). The orthogonal travel direction can emanate from any locale in the circular cross section and then likewise can interact (transfer its information) at any location in the eventual orthogonal cross section region. A wave can reach it's final destination anywhere in its structure ... from crest to trough ... and still transfer invariable information content regardless of where the interaction occurs along its wave form. This occurs because of the information relationship elucidated by the -Apollonian Hypothesis of topological information translation.
The comparable source/receptor sites are never "identical" ... even though our models and formulas assume that they are ... and so, what we take for granted as "actual" .... is actually a net-sum-median. By example, no two synchronized and phased photons emitted by a laser will strike a target at exactly the same location.
Any "values" assigned to a distance or duration need only meet "adequacy" requirements ... need only fall within some acceptable range ... in order for the factors or parameters to remain "consistent" ... and thus allow us to deduce net-relationships, as we conceptually organize experience and existence.
This holds true for Geometry or for any other human endeavor. "Standards" and other mutually shared "identities" become the focal point for elucidating "relationships". This is also relevant to the latitude range of Integrity functioning: optimum = ideal, yet, latitude = acceptable for practical purposes (to maintain and continue the function at hand).
~ ~ } I should make mention here that traditionally the original Theorem of Apollonius is interpreted in a slightly different manner. For any triangle with shorter sides a,b and longer C...a median line from the Angle ab to the midpoint of C, creating two equal lengths c, the following relationships exists:
a2 + b2 = 2m2 + 2c2.
This is notably a non-orthogonal general form equation, but is not as much to the point of Information Domain relationships as the Theorem is.
There is also a 20th Century Geometry formulation known as the SIMSON LINE. It is the "general form" for which the Theorem of Apollonius is a special "limit". In other words...the Simson Line specification ... pinpoints the crucial and fundamental nature of orthogonality in fluencial/dimensional relationships, and, in this set of geometric relationships, allows the angle defined at the circumference to take on values 'other than' 90 degrees. I.e., it sets up an ellipsoid! It defines elliptical orbital paths by specifying parallel orthogonal domains!!!
| Simson Line diagrams (in preparation) |
The Simson Line, deduced by direct information transcription along continuously connected linear and radial domains and /Apollonian relationships, establishes homogeneous and topologically identical and parallel domains; that are the underlying foundational continuums that link all the vector (information) forces of celestial mechanics deduced by Kepler and Newton.
Kepler Laws: 1) r = ed/(1+eCosq) 2) dA/dt = constant, L 3) 4p2 a/ GM
angular momentum L = MruNewton: a = (-D/ Mr2)(r) L = (Mr2) (dq/dt) (k)
a x L = (-D/Mr2)(r) x (Mr2dq/ dt)(k) = (-D dq/dt)(r) x k = (D dq/dt)(k) x r (reverse cross product
also reverses sign ± )k x r = dr/dq thus: a x L = (Dd/ dt) r = dv/dt x L {integrate both sides of equation}
gives: D(r + e) = v x L
then: Dr(r + e) = r x vL = M/M r x vL = L2/ M (since Mrv=L)
then: (L2 /DM) = r(r + e) = (rr + re) = (G + re) = (G + GeCosq) = G(1 + eCosq)thus:
(L2/DM)/(1 + eCos q) = G orbital ellipses
In a sequence of "general forms" progressing to a /functionally "special limit" at each plateau, the series would be
1) General Theorem of Apollonius |
Another analog that exists closer to home vis a vis particle physics, is the relationship between the Gauge Bosons. It is the relationship between the massive W and Z bosons, and their massless familial member: the photon. The compaction of a large-environment of "information" (the massive bosons) can fluencially compress (wave collapse) to a massless comparator. Where as, this produces a seeming imbalance - spontaneous "symmetry" breaking - as regards some kind of "mass"imbalance for particle "pairs" (where it seems odd that something so heavy is balanced by something so light), it can otherwise be viably seen as a reasonable dimensional translation mechanism.
It is interesting that a great deal of effort is made in tensor analysis to establish parameters that specify and fix orthogonality of more general ffunctions. Concurrently, boundary conditions and ffunction interrelations are sought, in an effort to specify how information spreads consistently and coherently through the rest of the domains of mathematical constructs. Higher fluencial formulations are worked out for how the entire rest of a system is affected when there is only the smallest variance in any single component of a system.
The trick is to keep equal scales in all directions regardless of spacial orientation. While concentrating on that relationship physicists attempt to show what happens everywhere throughout a system when even the slightest change occurs at any point anywhere within such a system! As complex and involved as this kind of arithmetic becomes, it all boils down to being a juggling act done with the mind. Impressive? Yes. Daunting? Absolutely. Intimidating? No. Mathematicians and physicists are merely doing with numbers and symbols what we do every day: walk the earth in balance and safety and equilibrium. A slight adjustment here, a coordinated effort there. Always aware of up-down, right-left, front-back. Sometimes turned to face one direction, sometimes another. Sometimes moving slowing, sometimes fast. Sometimes empty handed, sometimes carrying a heavy burden. Sometimes when the air is calm, sometimes into the teeth of a raging gale. Sometimes you can be so stably set that even if someone bumped into you, you wouldn't fall over, sometimes a bird landing on your outstretched arm while you are trying to balance on one toe, can bring you to the floor.
Tensor/metric mathematics is an identical process: keeping track of several groups of numbers and number relationships at the same time. It's just another way of keeping things together, organized and working while moving from here to there.
The only difference is how we understand and describe the factors involved. At the moment we are using symbols. The related dynamics will always remain familiar. Equal scales, right angles, the shadows that tilted or curved lines make on flat lines (and vice versa).
Valid function operators are not limited just to "D,d,d of <x>". They can include "D,d,d of <Axn>".
B2(Ca) = A2(Cb) relies on continuum-linkage with the mutual information pivot "k" (in the sense of the "excluded middle" of propositional logic).
now: f B2 generates T Cb = t
f A2 generates S Ca = s
s + t = Ca,b
s
0
S + T = å f(k) +
å f(k) = p/2
= (p (s + t)) / 2
0
t
The reference domain stays constant (s+t=C), but the sum of all the off-domain end point values of /(k) produced as s,t vary along the continuum sums to p/2. This is merely a variant of Cosa,b, Sina,b.
When s = t = (k) then 2å = p/2. å s,t,(k) = p/4.
This is the equal-scalarity sensitive orthogonal operator discussed above that translates and transcribes Cartesian to Conic, per re-interpretation of the Uncertainty Principle. {The "general" form can also be written using eccentricity as an adjectival variable of '.} Also, equal scalarity implies interchangability around the intersection of Boolean and NonBoolean functions: (g) + (g) = (g) x (g) {the localization where commutative and non-commutative functions intersect}. In other words, this is the Å form, whereas the previous was the Å form. An interesting interpretation follows from this. If we treat the summed momentums and positions (p,d) as contemporary scalars which can be interchanged {p=d}, then both can be substituted by
i
, and i2 = p/2. i = Ö(p/2).An important interpretation arises if we depict the two summations initiating a Hilbert asymmetry,
i.e., a spontaneous symmetry breaking:
around the point k=0 which floats along the string (s,t)
[ (0®s , t®0) ; i.e. (0®s , t®0) ; (® = -¬) ] ,
approaching or parting from the k=0 point will impart an appropriate positive or negative sign to the distance value; thus, one summation is always opposite in sign -/+ to the other. i2 is actually i x -i , and the result is i2 = -(p/2) , i = Ö-(p/2) .
This is where the alternating entropies of the nested Cantorian Infinities is introduced/displayed.
Within any domain the sign is uniform and therefore irrelevant and can therefore always be positive. Mathematical operations here are dynamically commutative. Once the operators are applied across exponential fluences, operators include non-commutative aspects in order to distinguish directional variances which become significant.
In his book Fearful Symmetry Anthony Zee describes the current state of "group theory" ... arcane physics understood supposedly by only the highest levels of the scientific community about the several different qualities that subatomic particles have. He makes a wonderful attempt to explain the balancing of primary-characteristics to the lay audience...and how those things can be expressed and understood in alternate (but compatible) ways. In chapter 11 he talks about the infinitesimally dimensionally-compressed entities called quarks, and how a juggling act of recombinations of them can produce a whole menagerie of other particles that end up being the ones we are more familiar with ... electrons, protons, neutrons, etc. At one point he presents an interesting mathematical equation to show the state of those relationships: "1 Å 8 Å 8 Å 10 = 3 Ä 3 Ä 3". This means that four families of related-characteristics ... adding their member-counts together ... will equal the value arrived at by multiplying together the number of quark-qualities in their familial combinations. This looks intriguingly like a trans/luencial Euler-Boolean relationship.
As you will read later in section Corollary Topics #16 of my presentation, I treat a variant of this formula. (i2) (4/p) = h/p2. This is an alternative method (per H.Puthoff: Zero-Point Energy) to place inherently-quantum operators inside relativity equations. h/p2 is not just an alternative "quantum" value, it is an information ratio mapped into a continuum represented by Pi squared.
The pythagorean theorem can now be alternatively written to expand multi-fluencial domains. The -Pythagorean Theorem is rewritten:
p
a2 + pb2 = pc2By explicit presentation of the (k) adjectival modifier (in this case p) in the matrix kAn we begin to expand the applications to real forces and real dynamics in the universe. This was already presented by Pythagorus in one of his later theorems. (k) could represent any given number or even irregular shape. As long as the factor is applied equally to all components, the basic relationship will always be true. Mathematically we call it multiplication. Linguistically we call it an adjectival modifier.
It is important to adapt the Pythagorean Theorem - and thus trig and tensor/metric equations - directly to information translation of orbital mechanics. The area of a circle is pr2. My tentative thoughts are that we can reorganize the Theorem as a linear-Cartesian-statement to being a conic-statement. The arithmetical relationships will still hold and we can manipulate conic "areas" and the interfaces (the planar conic areas generated where two sphere boundaries would intersect) more directly. This will probably be useful in evaluating gravitational-field strengths between masses and correlate with some LaGrange nodes.
a2 + b2 = c2
becomes pa2 + pb2 = pc2 !!!!!
then pja2 + pkb2 = plc2 !!!!!
The equation's complexity can reasonably be improved by replacing a,b,c with complex variables "a=ax+di", etc. Planar forces such as the force of gravity can then be translated more clearly. Also, the inverse square rule can be re-configured as a /function of p. In the old case (linear pythagorean) p was omitted because it was in the form po (ie, "1"). The force density which diminishes proportional to the inverse-square will also operate according to the inverse pr2 at appropriate /luencial densities.
When the linear distances between centers of masses are figured, the p factor fluence becomes zero. Off-center values can be determined when the fluence factor (ie, exponent) is not-zero, with proper use of chaos values for the equation. That is, non-digital exponent values j,k,l.
The values that get generated are the "force" of gravity between the masses at any points in a plane perpendicular to the line connecting their centers of mass. This becomes an initial technique for solving "many bodied" problems because it fixes values "off-center-line" of any two masses.
A correlation of the nested entropy values will probably also lead to a better understanding of why the inverse square law restabilizes at .37 just before the magnetic field of iron disappears (and "symmetry" relationships take over) as iron is heated past 700oC.
The next several pages will head into slightly more technical discussions. Since beginning the current version of this work in 1991, I've continued to do research and incorporate new findings appearing in the scientific literature. Recently I came across some fascinating material which I believe lends concrete support to my ceptual proposals. The more casual reader might want to skip ahead to the (*) on page 133 without any loss of continuity. In the meantime, I will correlate my proposals to recent mathematical analyses of Quantum Gravity and models of Chaos.
The literature I will be referring to are:
[1] "Weaving a Classical Metric with Quantum Threads". Ashketar, Rovelli, Smolin.Physical Review Letters;vol.69,#2pp237-230.
[2] "Towards a Statistical Mechanics of Spatiotemporal Chaos". Politi & Torcini.Physical Review Letters;vol.69,#24pp3421-3424.
[3] "Controlling Chaos in High Dimensional Systems". Auerbach, Grebogi, Ott, Yorke.Physical Review Letters;vol.69,#24pp3479-3482.
[4] "Algebraic Correlations in Conserving Chaotic Systems". Bhagavatula, Grinstein, YuHe, Jayaprakash.Physical Review Letters;vol.69,#24pp3483-3486.
[5] "...Improved Uniqueness Theorem for Quantum Fields on Space-Times with Horizons". Kay. Journal of Math.Physics;34(10)Oct.1993pp4519+.
[6] "Gauge-Invariant Formulations of Lineal Gravities". Cangemi & Jackiw. Physical Review Letters;vol.69,#2pp233-236.
[7] "How Efficient is the Langacker-Pi Mechanism of Monopole Annihilation?" Holman, Kibble, Rey. Physical Review Letters;vol.69,#2pp241-244.
[8] "Relativistic Classical Limit of Quantum Theory". Shin & Rafelski. Physical Review A;vol.48,#3pp1869-1874.
[9] "Observation of the scalar Aharonov-Bohm effect by neutron interferometry". Allman, Cimmino, Klein, Opat, Kaiser & Werner.Physical Review A ;vol.48,#3pp1799-1807.
[10]Quantum Philosophy". John Horgan. Scientific American;July 1992pp94-104.
> The work by Ashketar et al [1] has received the most notoriety lately because it crosses the vast conceptual chasm that seemed to forever keep separate the smooth-continuums of Relativity from the energy packeting of Quantum Mechanics. Instead of trying to inflict quantum methodology on relativistic equations, they created new quantum "operators" in an effort "to 'explain' from first principles how smooth geometries can arise on macroscopic scales."
I continue quotation {emphasis is mine}: "The purpose ... is to report on the picture of quantum geometry that arises from the use of loop variables. ... we must first introduce operators that carry the metric information {!} and regulate them in such a way that the final operators do not depend on any background structure introduced in the regularization. We will show that such operators do exist and that they are finite without renormalization."
The key here is quantization taken the next dimensional step, from its historical use relative to simple linear units per Planck's constant h, expanded to show that the plural-dimension "quantum unit" is a self-recursive loop. The loops are then shown to be "substantive", with the analogy that massive quantities of the self-consistent loops impinge on and interact with each other's phase spaces...and blend (by smearing functions) into unbroken unquantized continuums subject to Einsteinian Relativity.
The new "smearing functions" are written out, and then explained as: "fe(x,y) is a smearing function, a density weight 1 in x, which tends to d3(x,y) as e tends to zero and where gy,y' is any smooth loop that passes through points y and y', such that it shrinks smoothly to a point as y'µ y. ..on nonintersecting loops, the operator acts simply by multiplication."
This is exactly my previous interpretation of information transcription-translation between linear and conic domains. Linear quantae transcribe to self-recursive quantum conic loops by: "multiplication". Reliance is placed on meaningful and valid Limits being reached by ratio factors that converge at different rates. Differential integration in continuums of unequal scalarity (!). Ashketar continues: "..corresponding eigenvalues of area are then quantized in multiples of (lP)2/2." [lP is the Planck length]
"...multiloops are equivalent to single loops whence there is a well defined bra<D|." This produces a weave state of the loops <authors' evaluation>. It also calls to mind fractal-chaos math where all regions display identical topology, no matter how simple or complex, expansive or confined, enlarged or compressed {My observation}.
{In order to close the packing of the loops and establish smooth nonquantization, the authors require that the average distances between the centers of the loops exactly equal the diametric lengths. They describe that value as: the Planck length times the square root of p/2. lPÖ(p/2).
The same generic value I developed geometrically (sans Planck) for i.
Their value would translate to lP "i.}
> [2] discusses looking into different approaches for analyzing phase-spacetime chaos. I found their discussion intriguing because in their own way they tie together the limitations inherent in following Turing sequences. They also present strange attractors as localized entropy regions. {!}.:
"Coupled Henon maps are introduced to model in a more appropriate way chaos in extended systems. ... A further implementation of the z-function formalism reveals the extensive character of entropies and dimensions..."
"Direct integration of partial differential equations often requires a large amount of computer time, thus limiting the accessible parameter region." {That is, linear sequential evaluation is not always productive.} "Coupled map lattices [CML], characterized by discrete space and time variables, are better suited for simulation and still reproduce many of the interesting features exhibited by more realistic systems." {Plural dimensional simultaneous operations are more effective and time efficient.} To overcome the difficulty in previous efforts - distinguished by "non-invertible dynamics" - "...we introduce a lattice of coupled Henon maps."
In their presentation they "...consider <the math models> as a paradigmatic example for developing and applying thermodynamic formalism {entropy} to extended systems, in strict analogy with what has already been done for 2D maps."
They then go on to make a rather curious remark. They introduce "fictitious dynamics along the continuous "time" axis t". (!) Apparently, they felt the necessity to introduce an additional "temporal" component which couldn't be the "same" as the time-function already in use, yet had to be quasi-temporal in nature(!), so they called it fictitious(!)
And further along: "Assuming that the dynamical entropy Hi is an extensive quantity {i.e., the entropy of the whole environment}, it is convenient to introduce the density hi= Hi/L. ... the local entropy. Analogously, a dimension density ai can be defined from the local version of Kaplan-Yorke formula, (6), ... Rigorously speaking, relation (6) represents an upper bound to the exact local dimension. .... we are not aware of a single non-generic example where the bound is not saturated."
..."While the exact evaluation of z requires knowledge of an infinity of orbits, Cvitanovic showed that the estimate of b, obtained by suitably truncating the Taylor expansion of z-1, is often sufficiently accurate." They then give a summation equation for generalized entropy densities, explaining which component refers to the local entropy density within that summation, and finally refer it back to their z-function.
"The comparison ... shows ... the topological entropy density ... clearly reveals the stabilizing {!} effect of the diffusive coupling."
"If there are at least two different phases prevailing into distinct h regions {distinct local entropy domains}, then a phase transition can be detected as a discontinuity in a derivative of l(q)." .... "Now, we apply the same formalism to the estimation of fractal dimensions."
"This phenomenon is, in a sense, complementary to the phase transition observed in filtered chaotic signals, where the competing phases correspond to distinct stable directions in phase space: here, it is the unstable directions which distinguish the phases."
JNR: dynamic stability poised around a balance of several entropies and negentropies.
> [3] formulates "a feedback control that requires modeling the local dynamic of only a single or a few of the possible infinite number of phase space variables." In other words, they propose that extraordinarily plural dimensions are not a problem as they can be compressed/reduced/recodified to a single or a few dimensions for evaluation. (!).
"The novel aspect of the control mechanism we introduce here is that it can be implemented directly from time series data, irrespective of the overall dimension of the phase space." They go on to specify an unstable equilibrium state x/ linked with a scalar time series at some specific time i. They then do a most casual manipulation which is tantamount to creating separate temporal dimensions (!). "By decomposing the vector xi-x/ as a sum of the two vectors xi(s) and xi(u) lying respectively in the stable manifold (contracting directions) and unstable manifold (expanding direction) of J, the projection onto the x direction can be expressed..."
"Thus, even though the control procedure takes only a single direction into account explicitly, the actual phase-space trajectory in the full n-dimensional space approaches x/ asymptotically. The multi-dimensional problem is effectively reduced to a one dimensional one."
JNR: A reverse management of this analysis reveals that multi-temporal domains are eminently present - though masked - by the compressional translation. Without loss of effective participation or presence. Reconstitution of component vectors is valid.
They continue with a discussion of "noise" {sic: Information theory equates noise with entropy. Where the authors use "noise" I will substitute "entropy"}. There is a noise term hi. "A large {entropy} term may on occasion drive the dynamics out of the neighborhood of the fixed point where the dynamics is linear..." There is "...{entropy} originating in the time evolution of the system, as well as observational {entropy}."
..."In order to produce a convergent expansion which can be truncated, one must resort to embedding the scalar time series in a space whose dimension is equal to that of the unstable manifold. ... In general, there is an interplay between the dimension of the embedding space that is employed and the extent of the history that need be considered in order to achieve control."
> Citation [4] explores how standard algebraic analysis can mimic chaos formulations and vice verse. Their indications are, that in the "long-range", it is possible to find non-chaos expressions which can translate into findings arrived at through chaotic formulas, and vice verse.
JNR: This becomes particularly pertinent to my comparison of the biological chaos work of Stuart Kauffman and the non-chaos work of Rudolph Marcus.
>[5] by Kay, is another approach for blending quantum mechanics with relativity. The fascinating part of the discussion there is the recognition of two separate techniques of formulation (!). There is CCR and CAR: Canonical Commutation Relations vs. Canonical Anticommutation Relations. There is also reference to bounded and unbounded versions.
What impressed me the most is that this is principly a comparation of nonBoolean versus Boolean explanation descriptions, and an effort toward expressing a paradigm which can accommodate both ... as valid descriptors of quantum-relativity. (!). This is something accomplished by Nested Cantorian Infinities per Euler.
> In citation [6], discussion of Lineal Gravity concludes by mentioning that an extended "Poincare' model involves an unconventional contraction of the SO(2,1) model: Owing to the well known ambiguity of two-dimensional angular momentum..." and that "the de Sitter model can be obtained by dimensional reduction {!} of planar gravity...".
> [7] I cite only because it seems to runs afield of the Integrity paradigm evaluation of EM. There is an EM structure that Nested Cantorian Infinities seem to omit. That might be a mistake on my part if the [7] remark is unavoidably correct. My impulse is to say that the rest of the reference is wrong and that NCI is correct. All I can admit is that the disparity needs deeper evaluation. To wit:[7] "As is well know, all grand unified theories (GUT's) of necessity give rise to t'Hooft-Polyakov magnetic monopole solitons." NCI does not require an EM monopole. The only analog of such an asymmetry occurs at the tangent point of a plane-compressed conic (circle). And that is orthogonal to such an EM vector monopole. (refer: graph . page 119)
>[8] deals with dimensional compression of S into a singularity. Both the presence of S and its compressed forms result in groups of very specific well known functions. By holding a coarse grained Wigner function (which involves Boolean handling of Euler relationships of Q,p,i,S) it is possible to formulate a limit S| 0 and arrive at relativistic Vlaslov equations, and equations for spin and magnetic moment density.
>Finally, [9] deals with results of neutron interferometry experiments that confirm Aharonov-Bohm quantum predictions that potentials (even when no fields or forces are present) are sufficient to "change the quantum mechanical motion of the particles in the system". One of the controversial results is that coordinated "action-at-a-distance" can occur not limited by the speed of light. A change of quantum component for any one member of a particle-pair in the universe, simultaneously changes its "partner particle" no matter where it is in the universe.(!).
<Citation [10]> To overcome temporal-separation Bohm conceived of a "pilot-wave" that could informationally link particles to future or far-distant events, and affect their present configurations ... in anticipation of future interactions. In order to accommodate the multitude of potentials this presents, several ideas have been suggested. Gell-Mann proposes all past events should be consider as acausal and nondeterministic. D.Z.Albert of Columbia University suggests alternatively that previous experience creates a literal "mind-set" which predisposes what will be observed when the observation finally takes place.
A corollary situation exists within the mathematical framework for "light" per se, according to Maxwell's equations (on which Einstein built relativity theory). There is the "retarded" solution - which gives the time sequence of events as we know them. There is also the "advanced" solution - under which the effect precedes the cause.
The essential nature of the problem here can be reduced to our inability to specify exactly what energy/matter is. Light photons - representative of the qualities of energy/matter - display themselves (and can be described per separate descriptions) as either particles or wave. [Scientific American. July 1992 pp94-104]. A variety of experiments have been conducted using many different techniques including laser-beam splitters [Mandel et al; University of Rochester] and laser polarizers [Chiao et al; Univ.of Cal].
What comes out of these investigations is that there is no way to find out the quantum states involved without "collapsing the wave function" and ostensibly destroying the information sought. What is baffling is that if a polarizer is placed in the path where such a "collapsed wave" would have been, the wave reappears(!) and goes on to display normal wave interference effects.
JNR: What we have then is a group of mysterious real-existing properties which seem to contradict each other when we investigate those properties, yet don't present a contradiction when we leave well enough alone: wave vs particle, quantum vs continuum, gravity as a force carried by "particles" vs no particles found to carry gravity, "tunneling" which defies classical laws of conservation and resistance.
What we also have, is the need to look at these phenomena in new ways, to see if there is a way to rationally coordinate and explain them. There is. It is by the inclusion of multiple temporal dimensions ... which can individually be reduced (translated/coded/compressed) to an instant. Time as a "holistic-group" continues with extent and direction. Distinguishable dimensional arms (as partial derivatives) can collapse to "zero" length, and create the effects seen. And, as the following geometric evaluation will show, "collapsed information" is never lost per se, and can therefore be reconstituted. The experiments referred to above can be re-thought as having done just that ... having affected one or more temporal dimensions and therefore having produced results which display all temporalities (waves) or compress them (particles).
My contention has been all along that Gravity is the felt-force of interacting temporal dimensions. This meshes perfectly, as supported by a result in neutron interferometry found by Samuel A. Werner [10] of the University of Missouri at Columbia ca.1977 "the interference pattern formed by neutrons diffracted along two paths by a sculpted silicon crystal could be altered simply by changing the interferometer's orientation relative to the earth's gravitational field. It was the first demonstration that the Schroedinger equation holds true under the sway of gravity." Gravity is a temporal gradient field which affects the partial-differential temporal components of the particles within its effective region. Black holes cannot restrain gravity because it is not a particle (so-called "graviton") ... it is pure gradient.
This is crucial to recognize. Gravity must be a component of significantly different character from the rest of what we observe because it interacts differently from the rest. Gravity restrains everything except itself. That's because there is no "thing" to restrain.
(*)
The current reigning paradigm of photon/wave ffunctions is that "by definition" a photon has a singular-planar configuration, like a wavy line drawn on a flat sheet of paper. These waves are the Einsteinian structures that physicists now run through split laser beam experiments and polarization sequences. The polarizer experiments cited above (Mandel; Chaio) as well as the ones by David Finkelstein and by Aharanov-Bohm et al seem to point to events being connected across dis-continuities, allowing for action-at-a-distance, and the statistical appearance of events where they might not be expected in classical/deterministic systems.
The experiments runs like this: a beam of light passes through a polarizing filter. Some light is blocked, other light is allowed to pass. The passed-through light encounters a polaring filter placed 90 degrees (at a right angles) to the first filter. All remaining light is blocked.
Next, a third filter is placed in between the original two. Something extraordinary happens. Something previously unexplainable by classical Newtonian/deterministic mechanics, but very plausible via Quantum Mechanics. When this non-orthogonal polar-filter is in place between the first two all the original light exits past the third filter (!). The middle filter seems to affect the light stopping ability of the original filters. To deal with this enigma, quantum math's statistical methods are applied, with the attendant meaning that a third "variable" (the third filter) altered the possible states available for the light to be in and now allowed the light to show up again - randomly - at nonsequential locations. The quantum mechanical calculations based on statistics and probability allow for the appearance of things where we can't pinpoint a clear chain of events that would get them there.
This is a real monkey wrench if we try to hold on to the Boolean grail that a . (bar)a = 0. That Boolean equation implies that if you start with a full barrel and take out part of the contents, then remove the rest, there is nothing left. Now comes the photon three filter experiment which seems to say that if you take out just a little more (!) from the empty barrel...all the contents come back again and the barrel refills!
The only conceptual model physicists had to account for this experience was Quantum Mechanics (QM). QM doesn't predict what will happen, but it allows for what could happen. QM reasoning says that if you have already accepted a range of possible states for a given system, which runs from empty to full, then that range is never removed, and, if you arrange the appropriate mechanisms/conditions, any of the states can show up again at any time; no causal requirements necessary.
If we persist on using the current definition of a photon, with its current assumed information-configuration, then we do indeed see a miracle in the laboratory. A "miracle" that we can now use quantum mechanics to describe, but still not explain. Bell's Theorem (1964) made a heroic attempt to explain "non-locality" linkages, and several subsequent efforts have "validated" his premises and mathematical logic, all based on stochastic fundamentals. But there are intractable hurdles, whose resolution relies primarily on imaginary operators that are presumed to /function differently in higher-dimensional configurations than 4-dimensional spacetime. Bell (after Bohm) believed that some sort of guide wave exists which conveys to the actual wave its instructions on where to exist and what state it should be in. He tied this in with another requirement of Boolean Quantum Mechanics. There is a QM symmetry requirement relevant to fundamental particles which says that certain particle pairs must be in complementary states in order to fit compatibly with each other in special situations. Electron pairs (Pauli), for example, can co-exist in atomic shell energy levels if one has "up" spin and its partner has "down" spin. This is called Conservation of Spin-parity and is ruled by Newtonian "conservation" conditions (Boolean grail) applied through the Laws of Thermodynamics (equal reactions; energy applied = energy expended; etc.). It is possible to separate such electron pairs and then alter one of them from up spin to down or vice versa. In order to conserve spin parity, the other electron must embody the opposite spin state no matter where it has travelled to in the universe and at a "time" instantaneous with when the first member of the pair is altered. Like the light beam which suddenly appears where it wasn't expected or predicted (exiting freely on the far side of what were assumed to be barriers to its travel), there seems to be an additional situation (mandatory conservation of parity) where we have to allow for information to be transmitted with total disregard to and completely unrestricted by the Einsteinian limit of the speed-of-light. We seem to had stumbled into another even more compounded paradox: we either have Order, or we have Chaos, or we have some kind of Ordered-chaos.
In contrast, I aver that the -Apollonian percept can resolve this dis-parity. First, Heisenberg Intersections (HI) "fix" quite deterministically the subsequent energy patterns. The high "correlation" values which investigators have found between distanced events stemming from a singular locus - which neither subsequent test locales could have "informed" the other about, except via faster than light communication - is a result of simple separate HI affects. Coupling that falls back on simple 50/50 probability functions.
Second, part of the problem rests in an a-priori ceptualization of a photon as a two dimensional wave. I believe that all current analysis of photon polarization experiments which involve that basic percept, and which evaluations of experimental results rely on it, are built on the erroneous application of that image and of not being able to blend classical physics with a quantum-mechanical situation!
It is my proposal that all wave ffunctions are "stressed fields", in the same vein that Gravity is the felt force of stressed "temporal" fields. As such, photons do embody several orthogonal components (not just 2) - -Apollonian fluences (which may be in a zero-exponent configuration, therefore not "expressed" yet still present to interact with environmental encounters), and must react to other stressed fields they encounter. "Information" can be orthogonally compressed for any partial differential, and remain there, "coded" and condensed, until the next HI.
Current experiments, contrary to Heisenberg's dictum that all encounters affect all participants, treat photons passing through polarizing filters as being essentially unaffected by the polarizing material (!), except for straight absorption or linear reflection, and except when in perfect planar alignment with the photons. Heisenberg demands an adjustive interaction at all times in all occurrences. If we apply the -Apollonian structure to photons ... a self-Integral stressed field ... that naturally interacts towards entropic stress reduction when encountering any other "stressed fields", then we have a new way do evaluate the triple polarization experiment:
1) We define all waves as having orthogonal components, which might have different "expressed qualities" (eg, electricity vs magnetism) and may be configured with an exponential-zero fluence component <z-axis(?)>.
2) All energies, being "stressed fields", continually interact with other "stressed fields".
3) When photons interact with the "stressed fields" of a polarizing filter, a portion of the photons are absorbed, reflected or interference-phased by certain complementary or aligned components of the polarizer. All the rest of the light - as required via Heisenberg - interacts and is realigned by the polarizer's own bi/tri-orthogonal components. That is, the incoming photons are rotated and reoriented by the filter.
4) It does not matter what orientation a 1st polarizer has. A second filter placed orthogonal to the first will always block all of the photons because they have been aligned to be blocked by orthogonal phasing.
5) If an intermediary polarizer is placed in between the two orthogonal filters in some rotation not orthogonal to either of the first two, it will also re-orient the photons: to be non-orthogonal to the last filter. What happens is that each encounter rotates the "stressed fields" (ie:photons) along their axis of travel and align or un-align the photon's other bi-orthogonal components.
6) In the 3-filter experiment, all photons emerge past the third filter because they were causally re-oriented at each stage of encounter in the whole process.
As I will discuss later on in regard to different ways of evaluating Chaotic biological systems, a significant difference begins to show itself here. How we describe and understand a system is based upon the amount of information and interacting channels we ascribe to it. A system that is sufficiently integrated can be described by deterministic conditional change of events. If there is insufficient information, the system can still be meaningfully discussed. Only here, we apply statistical evaluation. Both techniques are valid. Both are "accurate", to the extent of the information available.
If a specific process-dynamics is an information "black-box" (exemplified by not knowing exactly what is happening between the polarizing filters, or the exact mechanisms of photon/polarizer interaction), then the only way to describe or discuss a system is to list all the observations and try to evaluate "what is possible" ... without knowing why.
If we enlarge our knowledge base - including the interrelational rete (interconnectedness) - of the direct and heterotelic components, then we can use causal analogues and methods to describe events. Sufficiency of information is the determiner of the appropriate methodology. Note that this does not invalidate the methodology not being used. This ceptual recognition merely helps us be more clear about frames of reference and how information affects "behavior".
For the newly defined photons, the polarizing filters become "the observers" , and the polarizers do in fact affect and alter what they "observe". They actively change the orientation component(s) of the incoming photons. We should remove our human ego from the evaluation. Though we are indeed the sentience which places the filters where they go, it is not our "intentions" that make the photons sit up and do tricks. It is the effort of our cohorts: the filters. In the same way that the Liar's Paradox harbored a subtly self-conflicting aspect, this experiment shows us that we have harbored a similar anomaly ... the unvoiced assumption that "we" are the agents of interaction. We are not the agents, the filters are. (!)
If we keep using the old definition of photons, we are forced to perceive that conscious human sentience "wills" the photons to behave in mysterious or unexpected ways. Two paired atomic particles will respond to each other no matter where they are separated to in the universe. Even at locations that require transmission of what their companion's state is beyond the limit of the speed of light to know about it. And "presence" allowed by statistical evaluations permit almost anything to occur.
Using the Information Percept of a photon - and requiring Heisenberg to rule - makes the 3-filter observations less mysterious and clearly understandable in a reasonably alternate way. Bell's majestic reasoning and mystical infusion may be re-evaluated as the best way to "explain" events when the core of the activity is a black-box mystery (a limited information group); when the black-box (internal information boundary) is filled in with perceptive ideas that model events (and the Total set of human information is expanded) then we might diminish the "mystery" but we afford ourselves a clearer perception.
In other words, we can't quote Heisenberg and end up with two more-serious conflicting results. He first stated that no changes occur without an interaction...at a locale. It is unreasonable to quote the same concept - when coordinated as it is with quantum exchanges of zero duration - to allow that zero-duration to now be applied regardless of the spatial distances involved. There is no conceivable mechanism which can dictate that such and such interactions will have affects at one (or several) other "there", and not some random "others". That is, if a particle with up-spin can impart to its down-spin "partner" particle anywhere in the universe, that it "changed", and its partner realigns accordingly, then every particle in the universe should be displaying the bizarrest forms of spontaneous change...not just the coordinated flow of local Heisenberg Intersections.
{addend Jan 1994: The February 1994 issue of "Discover" magazine contains an article titled "Welcome to Femtoland" that discusses the work by Dr.Ahmed Zewail who uses slight phase shifts in multi-frequency lasers to examine chemical reactions. Physicist Mark Rosker - describing what each light pulse looks like - is quoted as saying, "If you could freeze the pulse in mid-air ...you'd find it to be 15 microns thick and a couple of thousand microns in diameter." {!}
JNR: in other words, photons are not planar waves. They have components in more directional dimensions than just "two".} retracement...
We can coordinate the above discussion with other Heisenberg Intersections where definitve aspects of information, information transference/translation, behavior, knowledge, and prediction are important. One case involves the famous "thought-experiment" ... Schroediger's Cat.
Shroedinger designed a thought experiment that dealt with all moments called now as being Gödel Limits to knowable information. It was used in an effort to explain the correctness of using the statistical method of Quantum Mechanics to discuss unobservable atomic behavior, such as radioactivity. Without being privey to all the events inside atoms, we still must find some reasonable way to discuss and predict behaviors. One way is to amass sample situations. During a series of uniform time intervals, sometimes two events occur, sometimes ten, sometimes none. At some point we can begin making certain kinds of predictions based on what we saw. We may not be able to predict exactly what will happen or when during future intervals, but we can predict a range of statistically possible events. Exact sequential determinism can only be recognized after events occur. Before that we must allow for all potential possibilities.
This brings up the interesting twist amplified for us by Schroedinger. He conceived of a cat placed inside an opaque box along with a vial of poison gas. The vial is connected to a Geiger counter which is monitoring radiation emissions from an atom of Uranium. If radiation is detected the sensor will trigger release of the gas which will kill the cat. Schroedinger then asked "What can we say or predict about the cat? We can't predict with absolute certainty when or whether this particular atom will release it's extra radiation, so is the cat hidden in the box still alive or isn't it?" Until we actually open the box and make an observation we have to allow for all possibilities to exist at the same instant. That is, we have to throw away the intuitively accepted Aristotelian situation that either the cat is alive or it isn't. Until we have information to the contrary, the cat is alive and dead at all possible future moments called now. In one corrolary sense, our eventual interaction with the experiment will determine what happens. Our opening of the box to make an observation transfixes the matrix of events, one way or the other; the world becomes Aristotelian again.. Up until that moment though the Universe functions in quite a different way : statistically. The cat is alive and dead. Quantum Mechanics is a more proper way of describing the Universe than sequential determinism or singular cause/effect.
The statistical ranges of all possibilities used by QM is what allows for seemingly disjointed occurrances to happen, whether we can show a connected path of causal linkage or not. This is what allowed Bohm and Bell to link events that seemingly had no other direct connections. If something is statistically plausible, no matter how far fetched, then it cannot be exluded from consideration. If two factors infer that a photon can be either here or there, then a third factor permits someplace else.
The "Cat in the Box" has becomes the physicists' conceptual icon, exemplifying the sub-atomic world that behaves so strangely from our Newtonian experiences of cause and effect, and equal and opposite reactions. But let me take a moment to propose a Ceptual twist, a Pandora's Box of other issues, concerned with information, densely connected environments, and information access.
Let's make a really big box. Instead of a cat, take one of your neighbors or staff members, who knows about boxes (latches, construction, et al) and the experiment (with all its potential results) and knowledge about air and food and water and health and what it takes to ensure "survival" etc., and lets cheerfully put him or her in there. Let's see what we can say now about the life of the person put inside shall we?
Must we wait until an "outsider" opens the box to determine if the friend inside is truly "alive" or "dead"? Is the "state" of the "insider" only conditional on the Uranium? How does the "insider" evaluate the "probability" of being alive at each moment - or the next? Will he/she try to escape the Probability that death is imminent? Does the "probability" remain the same if escape is tried, compared with doing nothing? Does the probability of Uranium-caused-death keep increasing with the passage of each moment of hasn't-happened-yet ; and is the I-am-still-alive probability state progressively improved, balanced, or countered by having successfully punched a whole in the box (fresh air) and being in the process of unfastening the latch? Doesn't the fact that the "insider" can have an instrumental impact on the outcome require that we construct a whole new set of uranium-Geiger probabilities because the parameters change drastically .... according to how much information and how well integrated it is, that you or they recognize as existing in the "whole schema" ?????
I know this description complicates things. I know that it doesn't negate the concepts or simplicity of the original methodology. It does, however, describe conditions more accurately. We still have to deal with a better way of describing what we can or cannot say about radioactive emissions, but the presence of a multitude of interacting probabilities becomes that much clearer. (Isn't that what the original SETI calculations were all about?)
Where you set the "bounds" and the extent of integrated information interaction the system is allowed, determines the kind of mathematics used to describe a system ... whether statistical or deterministic. Both remain valid (eg Feynmann diagrams to categorize statistical enumeration). Turing machine mathematics have a value-to-humanity when the process for calculating stays within a reasonable time frame (continually being improved by new generations of computers). Statistical methodologies predominate when information and/or the paths of translation/transmission are beyond a present or "defined" bound (whether extraordinarily large or small).
Maxwell's Demon is another iconic creature of well intentioned but questionably defined boundaries. James Maxwell designed a thought experiment that placed a sentient imp demon at a mid-gate connector between two closed gas filled containers. He said that the demon could note speed, momentum and energy differences of all the individual atoms of the gas and could then open or close the gate as each atom approached, allowing high energy particles to pass in one direction and slower less energized particles the other. Instead of the gas equalizing at some stable temperature and density among both containers, the pressure and temperature of one would rise and the other would fall. All because knowledge and information could affect the system. His experiement showed that information could affect and disbalance uniform entropic dispersion and create negentropic asymmetries. Information put into a system could change it significantly. Brillouin came along later with some modifications to this idea, but the original tenet remained. In 1929 Leo Szilard evaluated Maxwell's Demon as "converting information into negative entropy" ... knowledge transferred via the interaction of "observation" enables subsequent actions ... including the ability to "re-order" (re-allocate; re-align) the participants." As a rule though if we mathematically assign a positive value to symbols representing Entropy, then negentropy and therefore information can be assigned an opposite notational expression (as designated and used by Shannon).
Again, a "truth" was discovered within the extent of defined conditions. Yet if those conditions are perceived in different environments with boundaries or interstices re-set, then the "truths" might change. The demon does bring a type of information into the system, but it is not the information of data-bits, which the previous analysis infers. Instead, it is heterotelic information created by the presence of new, different, and better reticulated information channels. The demon brings no added information or energy into the system in order to negentropically separate the high energy particles from the low. The information of each atom's direction, momentum and energy is there inside whether the demon is there or not. The demon brings no new data, rather, new channel locations and links. The "information" he uses is already present within the system in the particles themselves. What is added is heterotelic information: not new "information" per se, but a better rete of information and a mechanism that permits separation. Instead of particles imparting their energy/information randomly as they travel, at some locations conveyable information is directed through newly available and more complexly connected paths. Pre-extant information is focussed toward the completion of a task: enabling or resticting future locations for the particle to exist in. All the gas particles still impart information into their environment (each other and any surfaces within the boundary walls of the containers), but now work can be accomplished.
One way to make the Demon ffunctionally possible is to key on differences in the separate partial differential entropies of each particle. High energy particles would be allowed to traverse one gate because the momentum is acting out its entropy impetus for energy distribution. The low energy particles would traverse a second two-tiered gate in the opposite direction. Particles trying to pass through at too great a velocity would simply be too fast relative to the possible design of the gate; it might pass a gate activation sensor and arrive at the gate before that gate had time to open. Slow particles could have (or be accepted by) their partial derivative component fluencial-exponent aligned to zero and therefore be allowed to "tunnel" through or arrive synchronized for passage.
Whether this last musing is buildable or not, the bottom line conceptual relationship is. Energy and information within a system is available for manipulation and does not require external framing to be accomplished. "Enlargement" of the quantity of "information" can be effected either by incorporating more external data or by improving the heterotelic relationships and information linkages within a closed system. An elegant example is to compare a battery with a television set. In essence they both do one and only one thing: transfer electrons from an anode to a cathode. The manipulations that happen in between those two poles makes all the difference in the world.
The Demon - or other constructive devices - must be viewed as equally "internal" to the dynamic frame being discussed. The potential for re-ordering must already be present "within" the arbitrarily defined "bounds" of systems. The capacity to behave negentropically is already part of the natural dynamics of systems. Negentropy is not a contra-normal ffunction. It is normal and expected. The conditions that permit its display is what we are after.
Keeping in mind that what we think we perceive may not be exactly accurate to everything that is or is not present, I am reminded of the notoriety given by mathematicians and physicists to the concepts in Edwin Abbott's tale "Flatland" written in 1884. Most discussions I've read about it talk about the inability of a two-dimensional person living in a 2-dimensional world being unable to describe 3-dimensional reality ... the way we 3 dimensional people experience it. We in turn have the same difficulty envisioning higher value dimensions: 4, 10, 26, etc., even though mathematics infers the possibility of their "real" existence.
I also am reminiscent of my sophomore college days when I fancied becoming a photographer. A senior took a look at some of my photos and remarked, "Jamie, be very careful how you compose your pictures. Sometimes you'll find something on a print that you don't recall having been there when you snapped the shutter. When you look through the view finder, you've got to be the camera. You're attention may be only on the object and the image you want to capture, but you've got to be aware of what the camera is seeing ... everything that is there, not just what you want or assume only to be there."
The same seems to be true about "Flatland". All previous discussions express very freely about being able to live in a 2-dimensional world and being able to "see" squares, triangles, circles, hexagons, etc. The distinction being that flatlanders could never wholly see cubes, pyramids, spheres, dodecahedrons, et al. But, lets remember "seeing what the camera sees". In point of fact flatlanders never get to "see" any of those figures. The same way that no binocular human has ever or will ever see a "cube". I have never in my life "seen" any of these things ... all sides of a cube, or a sphere or any other 3D object at any given moment. Two information channels are insufficient to allow that ... at least ones placed so close together. I need at least 6 linked sensors in order to experience 3D objects. A flatlander would need at least 4.
The way things are, a flatlander could only experience 3 things: a point and its two extensions ... finite and infinite lines. Any other being it encountered would be a line segment like itself. Depending on the distance of separation between its visual sensors, it may or may not be able to distinguish between what the nature of any other line segment was. A "square" could just as easily be a "triangle" - with only one edge "visible". Examining what happened at a line terminus or juncture would be the only way to evaluate what it had encountered ... the change in angular slope .... closeness (distinguished by binocular information).
What a Flatlander could eminently do is what we have already done: that is, evaluate its knowledge of the world based upon "inclusion" or "exclusion" of information; the conditions that enable determinations and interactions. If it were a line segment and it intersected with any other entity, part of it might even vanish into the other. This might be good, this might be not so good. It would definitely be a "different" kind of encounter, to say the least. Regardless, a flatlander would be able to generate the same understandings that we have about "information".
Something about the universe is "objective" even in the whole swarm of individually subjective encounters.
Most importantly, we must be acutely aware that there might be more components and aspects to the conditions of an experiment or observation than we might immediately be cognizant of. By appreciating all the factors about "observation" - and the ways those factors become discernable - we can make a very specific statement about the nature of finding out "information" about something: that environment and conditions of an observation will affect what we observe, not just qualities of the item itself.
Consider a stream of water coming out a kitchen faucet at a rate sufficient to keep it a "smooth running stream". Under a strobe light we see it to "really" be a progression of discrete droplets. But, taking into consideration where and how we examine such water flow, we can appreciate that the water "flow", as a general rule, is not always in discrete droplets! When environmentally confined inside a closed tube, there is no surrounding air environment to permit a surface tension dynamic to affect the water as through air where we are able to visually examine it. Air is not a factor here, and the discrete water "particles" - which appeared when in a less confined environment - now function as they "really" are: a fluid/wave. (!?) Water molecules here interact without gas intrusions. Laminar friction, molecular compression etc are now factors.
Now let's keep these two aspects in mind and see what else we can say about what we observe. Slowly bring the side of a finger close to the steady stream coming out of any faucet. Your finger will become a little bit of the surface area that had been present inside the tube. When it just makes contact with the water there is an "instantaneous" change in the flow path. This is an effect caused variously by surface tension and by the Bernoulli Affect of fluid flow. Besides whatever else we can deduce from this observation, we can also conclude that any flow path - for whatever conditions or environment are present - will be the most kinetically stable one. This is a quality of Integrity behavior that in its simplest form appears as a rephrasing of the laws of energy and entropy. The difference is that we are heading toward formulating rules of complex behavior which follow smoothly from real world combinations of the isolated laws.
Water will behave discretely or fluidly or in a blended manner, depending on the nature of its environment, and, will exhibit dynamic stability appropriate to the conditions. In both/either locales (air vs tube) we see a specific phenomena. Water will exhibit certain behaviors under one group of environmental conditions and quite different ones during other conditions. We do not try to dissociate the behaviors and say that water must behave only one way but not the other. That would be ludicrous. The same holds true for our comprehension of the particle vs wave behaviors of matter/energy in the universe. Instead of trying to choose one over the other as the "true quality" of extancy we should refocus our examinations on the environmental factors which produce each set of observations.
Ergo: when examining the dynamic factors of a wave/particle - such as an electron - we are focussing on stability/instability situations of the wave form in general, and it is not unreasonable to model the states/shells as the image of reinforced wave phases, but, to not preclude passage through regions of transition or instability. Eg, the faucet water still had to pass through a spatial region between the plain-gravity-fall path, and the Bernoulli-surface-tension path. Atomicly we do not yet have the tools sensitive or fine enough to discern the transition motions and QM precludes that need for the present time.
Synchronous wave phase states are not the only factors at work at the atomic level, especially since most mathematical formulations treat waves in flat two-dimension. Off-plane affects to either side of a wave form, plus differences in wave compression at the peaks and troughs make for a panorama of subtle but important motion-changing forces that affect electron movements around a nucleus, for example. The simplistic Bohr atom becomes the Heisenberg quantum atom: dynamic self interactive bundles. Crucially, some "environment" is always at work. We can appreciate different environmental experimental-observational conditions depending on how much information and what factors we consider. We can evaluate energy phenomena as discrete particles when released from a self-defining environment. We evaluate the same energy phenomena as waves when more fluencial factors are considered. Systems and quantae and organizations have more qualities and aspects than we can evaluate at any one moment. This does not preclude the existence of other qualities, it just means that we should clearly understand that we only receive a small amount of information from any collective group of observations. Trying to explain the particle vs wave quality of atomic particles is like trying to explain a cube using a single moment of visual perception. With our 2 closely set binocular eyes we can never and have never ever "seen" a cubed structure in its totality. By relying on our given visual receptors alone we can never at any instant see the far side of a cube. We can only view 3 of the foremost surfaces. We wouldn't in our wildest imagination call such an object a "six surfaced thing which we can only actually perceive to have three or two or even one surface". My point is that we understand what a thing "is" by the totality of observed interactions, not by restricting ourselves to saying, "it is this and only this".
Finding a way to correlate all possible diverse observations we make about the world is what this whole presentation is all about. It is an attempt to find a reasonable and meaningful way to coordinate "diversity". Dimensions re-understood as fluencial domains interrelatedly nested, is a way of allowing the smooth transcription of energy and information into various coded forms, and seems a reasonable approach to resolving several scientific paradoxes.
One of the more puzzling aspects of our observations and derived
formulas that deal with "orbital mechanics" is why, in Space that is
"nominally" 3-dimensional, nearly all of the primary equations are vector
combinants in 2-dimensional planes? This is especially true of Gravity equations.
Aside from a unit vector that is "referenced" in the non-planar dimension, all
other forces balance in two dimensions at a time. The /Apollonian Geometry of
Information, in coordination with wave phase functions, not only show us the
crucial importance of orthogonality, but also act as "step-functions"
that strictly limit the "expression" of forces and relationships to orthogonal
fluences only. The potential exists for that special orthogonality requirement to
exist anywhere along the con/luences of
space-time. Therefore, non-integer fractal "fluences" should display
corresponding orthogonality relationships. And, just as "forms and geometric
shapes" differ between the different orthogonal exponent levels of integer-fixed fluences,
the same should be expected for the non-integer fractal forms and geometric shapes. Later
on this will allow some important considerations to be applied to those fractal
relationships.
Starting with the primal fluencial form, the point, which is x0, we arise the x1 form, the Cartesian linear continuum and its representative subset: the "segment". We now rigidly fix that segment, and treat it as a hypotenuse of fixed length. The circle, the next higher fluencial representative form, can be generated as the set of all points where any two lines that pass through the end points of the hypotenuse cross in the 2-fluence plane, at an orthogonal right angle. Importantly, this triangulation method produces 2 special situations, where one of the 2-fluencials collapses back to "0". It specifies "Orthogonality" and points up the crucial relativity in information comparation between fluences, via orthogonality. It specifies the next highest 2-fluencial form. It retains a linked continuity in all individual specification of values (by "direct contact" of components used to determine result values); and it can establish comparative information mapping, that is a familial mathematical cousin to "eversion of a sphere" (mathematically turning the surface of a sphere inside out).
ö
luencial analysis, as it eventually relates to poly-fluencial time structure, is crucial in describing and understanding such varied topics as topological sphere-eversion, reflection, and, the Laws of Thermodynamics.From "A Mathematical Mystery Cruise" (Peterson, 1990.p.51-52): "..at various times during a sphere eversion, there are a number of 'double' points {my emphasis} where two surfaces intersect". Peterson writes out the generic formula in "Mathematical Tourist" (1988,p.95) when he discusses the Hopf Map, dealing with topological projections evaluated by German mathematician Heinz Hopf:
"..each point (X1,X2,X3,X4) on the three-sphere {hypersurface} becomes the point (x1,x2,x3) on the two-sphere, where
x1 = 2(X1X2 + X3X4) x2 = 2(X1X4 + X2X3) x3 = (X12 + X32) - (X22 + X42) |
Note that all terms on the left are exponent-one where as all terms on the right are exponent-two {either linked "squares" or cross matrixed equal scalarity vectors}. Distinct separation of fluencial expressions. The "equalities" are thusly "translations" rather than "equal values".
When treated from a linguistic point of view "eversion of a sphere" is a description of fluencial compression (smoothing or simplification), in order to avoid a forced cusp (a problematic local limit that is eventually reached in such equations) that occurs if you stay within the complete set of original fluences. It is as if one of the point-locations which localizes the dimensional variables is brought down to a "constant" (zero, nee "one") that avoids an anti-symmetry factor from the equation. Eversion can then be accomplished, because a direction vector that would normally force a cusp in the later stages of the mathematical effort, is arbitrarily "removed" from the equations....and then re-arbitrarily "re-introduced", to effect "right becoming left" or in this case "in" becoming "out" and vice versa. Dropping down a fluencial step allows us to produce a "spontaneous" momentum reversal, that has no otherwise predictable causal presence or existence; and additionally had masked the sheer existence of distinguishable distinct fluencial transition techniques.
Lets imagine the process by using an analogy. Start by thinking of a flat Mercator projection of our world onto a sheet of glass. If we flip the glass over, and assume this view to be just another conformable representation of a randomly projected surface, we have no problem in reconstructing a new "globe". A smoothly and comfortably eversed 3-fluencial Earth. We mirror-image, inside out, by compressing three global fluences into two flat fluences and reconstitute it back, loosing no information along the way, but, reversing all relative positional values.
Further, assume a physical reality to the exercise of doing the same thing to a circle (two fluences) across a line (one fluence) that acts as the pivot of translation, just as the mercator (or any other map) would be a fluencial translating plane (or surface) for 3-space. Assign a directional time value on the starting momentum side of the reflecting diameter line, that allows you to 'move' in a positive 3-space value as you curve the circle rim back through the pivot line, (as if you were curving a planar sheet of paper). Holding the remaining part of the circle on the other side of the pivot steady, the starting side is heading towards a diminished radius of curvature, until it reaches a "critical point"...the pivot. Imagine the circle to be a smooth continuous domain where when we assigned a positive directional momentum (time) value to one part of the circle, it was mandatorily assigned to the whole structure, the remaining side of the circle immediately on the other side of the pivot now experiences the pivot, not as a transitional "doorway", so to speak, but once the rest of (i.e., the first part of the circle that is being transformed)passes through the pivot, and there is nothing left on the far-side to follow, the second part of the circle is required to 'pass through' the pivot with a spontaneous change of original momentum.
In one way of thinking about this, a spontaneous cusp is formed, where in order to go "forward" you have to go backward by an assigned equal and opposite time (momentum) value. M suddenly becomes -M. (Whoops, is this possible?....Yes)
Mirror phenomena that we take for granted, masks the existence of defined multifluencial time. Masked collective asymmetry. Asymmetry that can be made to appear symmetrical ... and vice versa.
Momentum in any given direction is distinct from momentum in any other direction. I face a mirror. Holding my right hand to my chest I move my hand and arm horizontally out to my right side. I cognatively recognize the energy and direction of movement, and note, mentally, that I am comfortable in seeing my reflection in the mirror and adjusting my perception of "that other event" and call it "the same" as me physically. It represents another way of me seeing "motion to the right" even though I know that if I saw another person in that place doing that motion, it would be "motion to the left".
I walk around the mirror and stand where that reflection would have been if it were a real 3-space person. Again, I move my hand from my chest, to the right, out into mid-air. But the real time-bound momentum motion does not match the mirror image I saw previously. What I had seen as "motion to the left" when reflected, I had allowed to be assigned the value of "motion to the right" in order to comfortably correlate it to my physical reality. But for a 3-space event, in that particular location, positive motion in a linear time reference, is negative. But since a "motion to the left" is a positive motion also, you have to either say randomly only one is positive, or assign a separate positive time value concurrent with a real fluencial movement. Keep vectors distinct. ie, fluencially separate.
The Laws of Thermodynamics that speak to conservation of momentum are just another way of our seeing higher fluencial time systems in a four fluencial (3-space, 1-time) 'mirror'. I see my arm move in that mirror reflection, in "an equal and opposite" direction. Force - a deflection or bending of time fluences - does happen in equal and opposite vectors, and both stay 'positive' in the time fluences they represent.
Why? Because time fluences are a Hook's gauge and elastically seek entropic smoothness and contiguousness with each other...maintain the lowest negentropic distortion state, the lowest energy levels. Orbital mechanics shows us the strain. Here we call it "Tidal forces". Tidal forces are structural stresses due to time field variances on a given mass, that in and of itself exists most stably when in its own time-well. Cumulative time well differences from significant mass structures distort fluencial uniformity relative to any one body's center-of-mass. The gravity well, that is the temporal-fluencial well, is no longer spherical, but a distorted ovoid when multiple bodies are involved, with each part of the affected body in force variance with its lowest energy state. Obviously the greatest distortion is in the direction of the combined center-of-mass of the multiple bodies.
Temporal stresses on molecules generate increased motions as particles start sliding down the slope of temporal well distortions, and thus heat is generated as a result. At some point molecular/chemical interactions become significant and energy production becomes the result of non-gravitational forces directly. Although, temporal aspects of chemistry probably come into play.
The ceptual world view that we are building extends to understanding why gravity (and the old image of the photon) reduce to planar states. The best corollary is the magnetic field, though instead of there being a bipolar field, there exists a self-referential "stress-field".
Imagine a bar magnet orbiting a larger bar magnet. Starting from any random orbit of sufficient momentum, the orbiting magnet eventually will be forced into an equatorial orbit with its poles aligned with or against the larger magnetic field. A temporal "stressed field" - which we call Gravity - is similar but more generally designated because, by not being bi-polar, its "equatorial" aspect is structured by its mass relative to its center-of-mass. A neutral orbiting body is affected uniformly on either side of the plane of rotation because the temporal stress densities are balanced there, and there is a singular stress factor - the Mass - which extends equally in all directions, but ffunctions fluencially in orthogonal relationships relative to extraneous masses. The "stressed temporal fields" of any and all masses interact together to reduce the stresses - ie, move towards the lowest entropy state (the lowest common-stress state), and the bodies interact accordingly.
In the mean time, we ascertain that "space" may not necessarily be "bent" by dense gravity. Rather, temporal components alone - molded by the elastic tendency toward lowest stresses and highest entropy - establish the restrictive channels of "highest stability" through which energy, matter, and information can transit.
Now we come to the next facinating plateau, a comfortably graphic one, at that. Seeing these novel "informationally" connected continuum relationships, we are open to new ways to get into 3-Dimensionality (sic)! A quick review reminds us that to go from X0 to X1, we have just one method to go from "point" to "straight line". To go from X1 to X2, we have two connected approaches: from a point that becomes the focus of the conic circle, OR, from a point that becomes a member of the circle manifold (its circumference).
This is a crucially important aspect to understand, because it relates to the biased prejudice reigning in modern physics/mathematics: Symmetry. The bias on which all current physics is built might be called their version of the heliocentric model of the solar system. There is (after, Reimann et al) a reliance that frames-of-reference and symmetry are referenced only to axial rotations through an axis or internally central focus. In higher dimensional analysis and consistent mathematical systems, these symmetries are found in "balance" at several plateaus. No matter how you turn or rotate some of those mathematical constructions, they will look exactly the same and behave the same way.
But once you start working with fluencial constructs, and recognize mathematical behaviors for arising the heterotelic relationships from one fluence to an adjacent fluence, then "direction" becomes a process superior to symmetry.
"Source locus" becomes the basal Identity, and can extend in many possible ways. The old system uses Pythagoras (trig-linear description) to describe a circle as the collective of all locations equidistant from a given point. This gives the "symmetry" paradigm of current physics. In contrast is the Apollonian (trig-harmonic) description, where the circle is the collective of all locations whose value is sine or cosine from a given point. This is the foundation of all the math of modern physics, which is in contradiction of its symmetry paradigm.
To go into 4-fluence (3 dimensions) and beyond, we can now show a panorama of optional information paths!
Developmental Sequences of several
Exponential
Continuums (fluences) from a fully Dimensional Point Locus
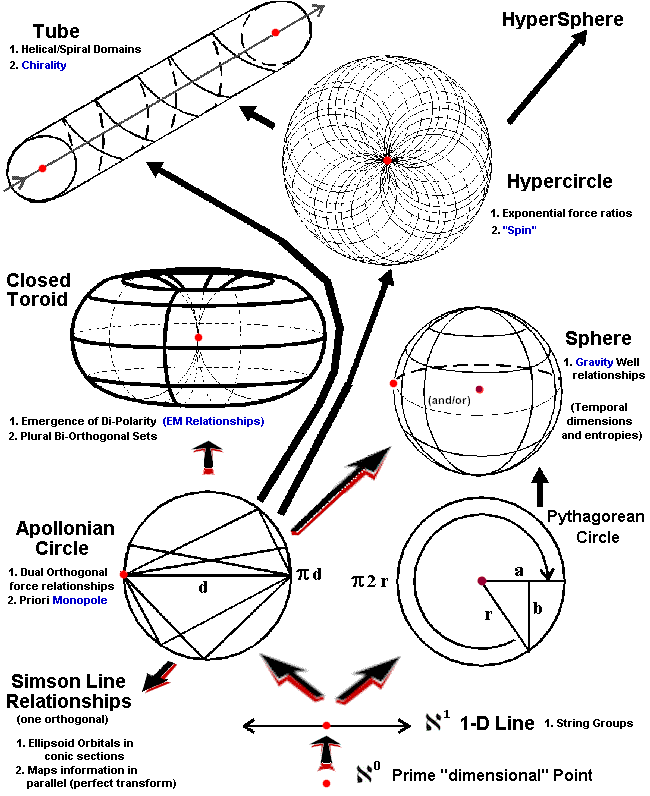
Process Result 1. Rotating the circle on its axis diameter
-----> sphere 2. Rotating the circle on its axis diameter
----->
sphere 3. Swinging the circle in the plane around
-----> hyper-circle 4. Swinging the circle into 3-space around -----> closed toroid the circumference point (5.+) The above are primal limit forms. Familially, other fluencially |
The wonderful thing about these relationships is that they generate conic section laminar models of the fundamental forces. Candidly, at this juncture I can only knowledgeably speak about Gravity and Electromagnetism. But I "intuit" that the other relationships will be valid also [plus, for Confluencial continuums that extends into "4th" and higher] in modeling the Strong and the Weak forces.
Point-Line-Circle-Sphere generates Gravitational relationships
density gradients
planar orthogonal forcesPoint-Line-Circle-Toroid generates EM relationships
Faraday self-inductance
bi-polarity
3-space orthogonal forces
One of the more obvious supports for the treatment of all space-time-energy as variable forms of Information, and their expression in "Existence" as Confluencial Relationships, is all the substantive work that was accomplished in the first half of the 20th century, especially by Planck, Bohr, Heisenberg, Yukawa. Information gets "translated" comparatively through exponentially fluencial domains. The inverse-square rule expresses the fall-off of tensor-elasticity along a simple linear (1-fluence) domain. When, however, those "linear Cartesian" values (between 2 points) are expressed as a single value in terminology of a 2-fluencial domain (a pure symmetric curve...the Circle), the elastic tensor fall-off increases by the translation value between the 1-fluence and the 2-fluence. And what is that translation value? It is the geometric progression of "kpn". Where the linear 1-fluence value is "h" Planck's constant, its "information content" is translated into the collection and summation of all values at all points equidistant from the focal-center-of-mass ... the surrounding circle, by division of the geometric progression translator: 2p1 ! Producing the standardly used "equivalent" form of "h", which is S , h-bar!
Another aspect of expanded-symmetry (see #11 next section) relates to specificity of the fluencial domains. When waves are described quantum mechanically as "collapsing" they could in fact just be fluencially compressing or transcribing. This relates to tunnelling phenomena, and is a crucial new way to perceive subatomic behavior. "New Particles" may indeed be the multitude of variant value states that the malleably interactive fluence values can take. Each represents an Integrity condition ... a balance of dynamic stability per the several fluences present, which certain energy quantae can take. A particle/extant still follows conservation rules if it "self-condenses" ... if it coherently re-organizes one set of fluencial entropies into another. Symmetry becomes a boundary condition for the entropy of any given fluence.
[end Part 12] 2025 Copyrights ceptualinstitute.com